今年的游戏时长（截至今日）上升到了 670 小时，如果在圣诞元旦假期稍微“努力”一下的话，说不定能超过 2022 年的记录。于是顺便统计了一下过去几年的游戏时长。

主要原因是今年玩了好几款“大部头”游戏，例如《博德之门 3》的游玩时长就超过三百小时，即使把属于去年十二月的八十小时除去，也占了今年总时长的三分之一。所以单从时长来算，我今年的个人年度最佳游戏也必须得颁给它了！

今年阅读比较不毛，因为看完了《大剑》全套 27 卷，所以日文阅读量尚可，但若除去漫画，总体数量似乎是近些年最低的，正好简单统计并绘制了一下过去 7 年的阅读数据。

此外今年实体书与电子书的比例正好是 2:1。总之数量下降所以书单和总结的工作量也就减小了！以下大致按评分介绍一下今年的图书。原本觉得今年可能没有六星推荐的图书，但是看了一下往年的六星书，不禁怀疑是不是自己变得更挑剔了，于是对前面几本评分做了一下微调，升级为六星。😛

这是他的青春 留下
留下来的散文诗

从若干年前起开始用“冷门歌手”孙燕姿的歌作为年终总结的标题，一直持续至今，结果今年 AI 孙燕姿突然火遍大江南北，网友用她的声音素材训练出生成模型然后去翻唱各种风格迥异的曲目，一下子扩大了我年终总结用的曲库😅。这里用《父亲写的散文诗》，因为今年回了一趟国见到父母，他们的性格脾气还是老样子，但面容上却突然间多了许多岁月的痕迹——但也不能说是“突然”了，因为签证 + 疫情其实前后耽搁五六年没回去了，所以这次回去非常开心，更开心的是 2023 年终于不再是“宅家的又一年”，去了日本韩国墨西哥，也算知足了。

今年通关的游戏总共只有 5 款，相比于去年的 23 款似乎是大幅下降，但考虑到去年是完全宅家，而今年出了好几趟远门，另外从总时长来看，相比于去年的 682 小时，今年的 511 小时也并不算少（这个数字在年末最后几天假期还在因博德之门 3 而持续飞升中）。所以其实今年玩游戏的热情一点也没有减少，幸运的是市面上的好游戏也在持续不断地推出。并且今年这几款通关的作品都是全程与 N 一起玩的。

我个人今年的年度最佳游戏要颁给《境界天火》，感觉给我打开了新世界的大门，体验到了机甲和射击游戏的乐趣；同样让人打开新世界大门体验到以前未曾接触过的游戏类型的游戏是今年 The Game Awards 官方的年度最佳游戏《博德之门 3》，但是鉴于通关还有一段时间，就放到明年的列表上吧。此外《王国之泪》虽然由于上一作过于优秀导致新鲜感没有那么强，但是依旧是做出了非常厉害的创新和超越！

今年很懒，都没有做季度图书总结，整年的书单都放在这里了，正好做一下大致统计，总计读完 57 本书（中文 20，英文 22，日文 15），但是其中有 9 本是漫画，还有不少艺术类书籍，所以总体大概和去年（42 本）差不多。这当中大约三分之一是电子书，特别是最近发现微信读书平台其实各方面都还挺好用的，也能很方便地在电子墨水屏的安卓阅读器上安装使用之后，在上面看了不少中文电子书。

A pen and pencil and paper is nothing if you have nothing to say. Otherwise do pretty watercolors and forget it.

《Reportage Illustration: Visual Journalism》是一本介绍 Reportage Illustration 的书，Reportage Illustration 按照字面意思翻译大概应该叫做“新闻插画”，但也许称作“新闻速写”更恰当一些，它可以归类到 Visual Journalism 下面，基本上是指新闻或者艺术工作人员通过现场作画和记录来报道某一个具体的事件。我最初了解到这本书以及这个行业是在公司的艺术兴趣班的一个叫做 Visual Journalism 的课上，老师带着大家一起去各种不同的场所，例如音乐会、咖啡店的脱口秀表演、户外甚至是一起观看某个著名的视频演讲等，然后让大家通过速写和文字结合的方式对现场体验进行描绘和记录，关键并不是要画出多么漂亮的画，而是要通过速写的方式记录下当时的氛围、声音、色彩、对话、天气等各种感官体验。

整体而言还挺好玩的，虽然和照片甚至录音录像相比通过速写能记录下来的信息量极少，但正因为能记录的内容有限，我们需要舍弃大量东西，反而导致我们记录中的内容是在现场令我们印象最深刻的体验（当然要做好这一点也是需要经过许多训练的）。所以再回去看自己当时的涂鸦时可能更容易重现现场的感触和记忆。然而这针对“个人”而言很合理，但是如果读者不是未来的自己，而是作为真正的新闻报道那样的形式给呈现给他人的话，看到杂乱的涂鸦和速记时能够重现的氛围体验有多少就很难讲了。所以我读这本书的一个疑问其实是这个行业究竟是如何存在的。

一天有多长
是不是无所谓混着过
像大人的世界

2022 依旧是宅家的一年，不过心里还是默默地希望这是宅家的最后一年，虽然家里逐渐被优化得非常舒适，而且不喜欢社交但又不善拒绝的我能以居家为由推掉许多不是很感兴趣的社交活动，但是当我开始准备年终总结，去翻看自己的照片的时候发现竟然无法轻松找到一张好看的图来做封面，仿佛听到一声警钟，在说如果再继续这样，可能就要永远这样了。永远宅家不出门当然不是本意，但也许是时候该认真思考如何迈出第一步了——也许可以把它作为新一年的议题，至于现在嘛，我决定让 AI 来帮忙，用 Stable Diffusion 来为我生成一张封面图。

自从疫情期间入坑游戏主机以来，自己也逐渐变成了一个【伪】资深游戏玩家，玩过了不少好游戏，感觉可以专门写一篇年度游戏总结。2022 年玩了 23 款游戏，其中 11 款 Playstation 游戏，12 款 XBox 游戏（7 款来自于 Gamepass），总计游玩时间为 682 小时。相比去年四月购入主机到年底就游玩了 500 小时，其实是放缓了节奏，一方面今年有一些时段在其他事情上花了不少精力，另一方面确实也是最棒最对胃口的游戏其实是玩一个少一个。

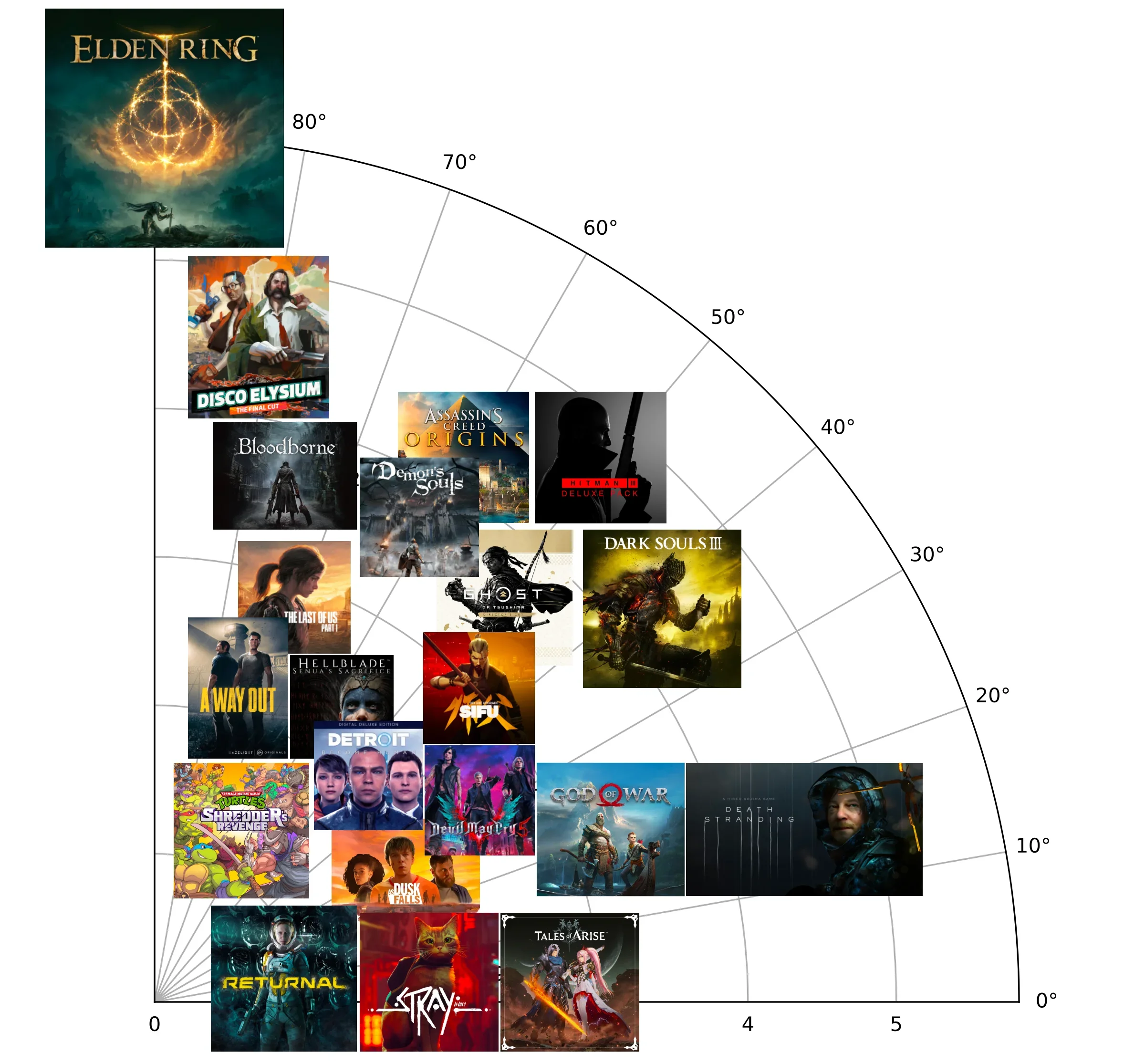
今年对自己的游玩记录做了一个粗略的统计之后，发现有一个简单的指标可以用来刻画游戏（在我心目中）的好玩程度：用游玩小时数 H 除以游玩天数 D，数值越大说明该游戏越让人停不下来，此外还可以将游戏的总时长作为辅助分数。下图中我在极坐标中以 atan(H/D) 为弧度，log (1+H) 为半径将这 23 个游戏画了出来，越靠近左上角的游戏得分最高。

今年从九月以来除了艺术类书籍和漫画之外，其他书似乎都没有特别惊艳，这里简单补完一下冬季书单。

总有种感觉今年读的书比较少，所以一直没有整理书单，不过大半年过去了好像也堆积了不少书目。首先介绍几个有趣的“故事书”吧。