最近需要 visualize 一些三维的曲面数据，于是简单调查了一下 Python 绘制三维曲面的一些常用的办法，贴在这里以免自己将来再需要用到的时候又想不起来了。比如我们想要画这个样子的 3D 曲面图。

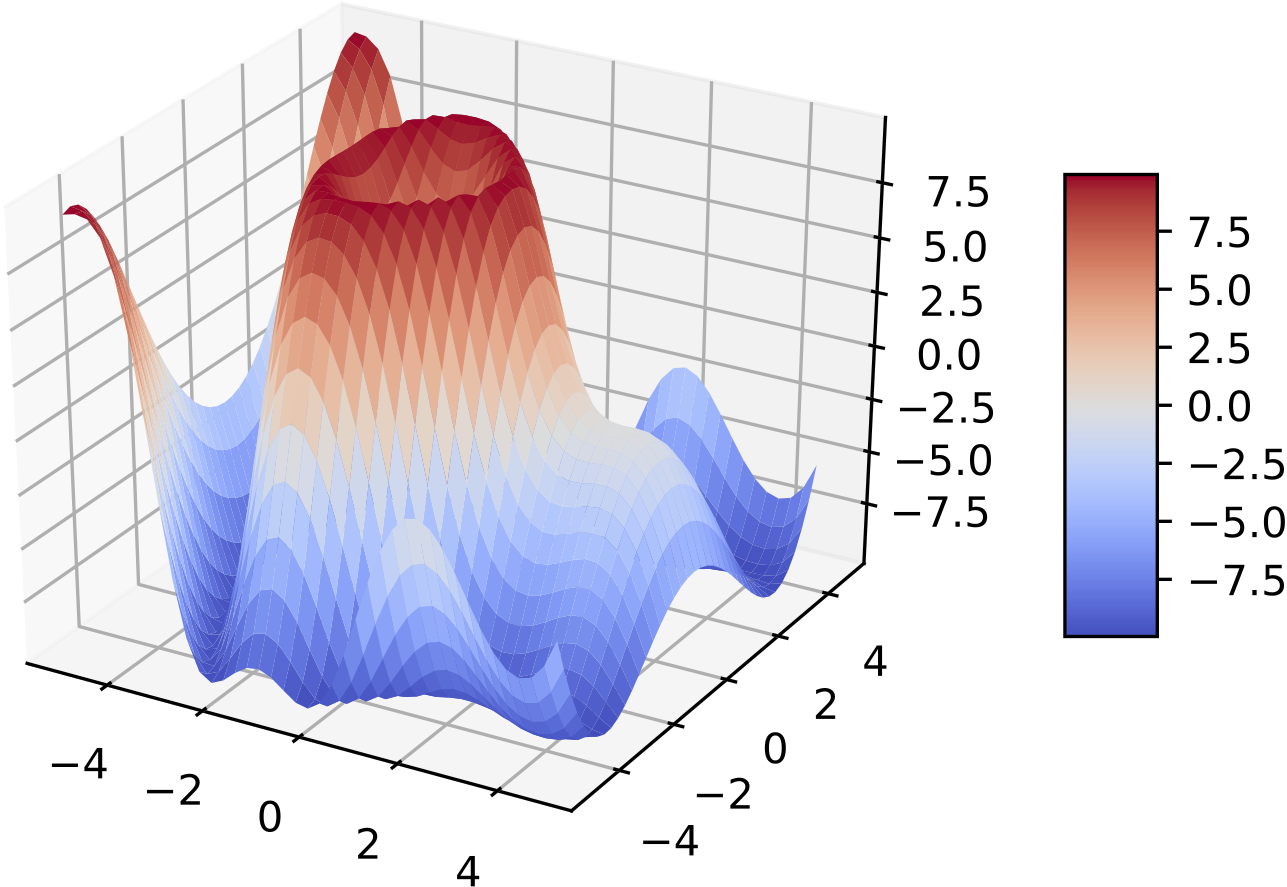
方便起见，我们假造一个 user case，假设 $x$ 和 $y$ 是两个 hyper parameter，现在你使用 grid search 的方式尝试了每个参数组合下的模型效果。

import numpy as np
def eval_params(x, y):
  # ...
# Make data.
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
Z = np.zeros((len(X), len(Y)))
for i in range(len(X)):
  for j in range(len(Y)):
    Z[i, j] = eval_params(X[i], Y[j])

现在我们希望把这个参数搜索的曲面画出来，看看最大值最小值、曲面的连续性之类的性质，所以我们需要画一个 3D surface 图。比较新版本的 Matplotlib 其实已经有挺好的 3D 绘图支持。上面的示例图其实就是在 Matplotlib 里画的。

import matplotlib
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm
fig = plt.figure()
ax = fig.gca(projection='3d')
XX, YY = np.meshgrid(X, Y)
# Plot the surface.
surf = ax.plot_surface(XX, YY, Z, cmap=cm.coolwarm,
                       linewidth=0, antialiased=True)
# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.savefig('surface.pdf')

其中 import Axes3D 那句虽然没有直接用到，但是如果删掉的话在创建 3D projection 的 axes 的时候就会出错。plot_surface 这个函数负责绘制 3D surface，参数相当 straightforward。因为 Z 作为我们 evaluate 参数的结果是一个二维的矩阵，所以 plot_surface 需要的前两个参数也是二维矩阵，并且需要是和 Z 大小相同。

简单来说，对于一组 index (i, j)，XX[i, j], YY[i, j] 和 Z[i, j] 一起给出了一个位于曲面上的点的三维坐标。而 meshgrid 这个函数就是用于方便地根据原来的 X 和 Y 来创建这样的二维矩阵的。

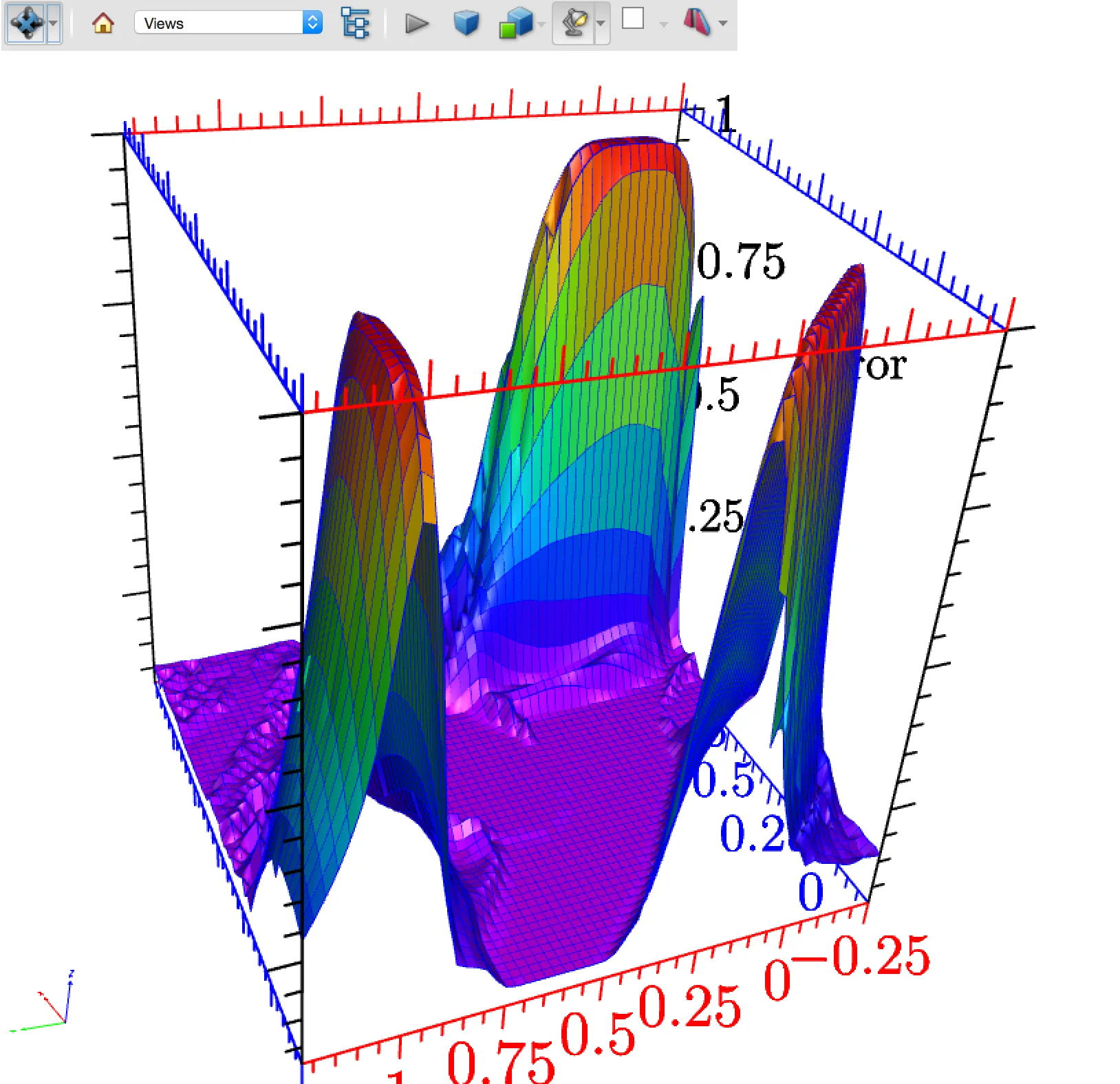
到这里我们的目标其实已经达到了。如果把上面的 savefig 换成 plt.show() 的话，会弹出一个对话框来显示 3D 曲面图，好处在于可以对曲面进行旋转、缩放等交互操作，有时候对于看到曲面被挡住的部分来说非常有用。不过 Matplotlib 的 3D 操作交互反应速度相当缓慢，可能是没有用任何硬件加速之类的简单实现吧。如果你不能忍受那个缓慢的交互速度，或者需要将生成出来的图片发给别人看，而对方又不一定是能运行 Python 代码的，那还有一个选择就是生成内嵌 3D 对象的 PDF 文件。PDF 文件可以通过 PRC 格式内嵌 3D 图像模型，不过目前只有 Adobe 家的阅读器（比如 Adobe Reader 或者 Adobe Acrobat）可以查看这种格式的对象。在 Acrobat 里打开大概长下面这个样子，可以对 3D 曲面进行各种操作和检查。

不过 Matplotlib 本身似乎并不支持直接输出这种内嵌 3D 对象的 PDF 文件。这里我们可以借助另外一个叫做 Asymptote 的绘图工具。它其实是一种绘图语言，和 LaTeX 结合得比较紧密，但是和 PGF/TikZ 或者是 PSTricks 不一样的是，它并不是实现为 TeX 的宏包，所以它的语法并不是一些看起来像英语一样的很飘逸但是一不小心就会语法错误的 DSL，而是有点类似于 C 语言语法。很多年前用它画过一些 3D 的 vector field 之类的图，感觉比较适合画一些复杂的 scientific 的 illustration，可以看一下它的示例。

当然我一般不会用它来 plot 数据图，不过这里可以借用一下的是它能输出内嵌 3D 对象的 PDF 文件的功能。Asymptote 画图的简单流程是创建一个 foo.asy 文件，把命令写在里面，然后执行

asy -f pdf -o foo.pdf foo.asy

就可以了。Asymptote 里构建一个 3D surface 可以通过一个叫做 surface 的命令来实现，它的第一个参数是一个描述 surface 的函数：输入是 $i,j$ 两个 index，输出是一个三维坐标 $(x(i,j), y(i,j), z(i,j))$。这个比较适合画一些 parametric function，不过这里我们是直接 plot 数据，其实只要做一个简单的矩阵查表函数就可以了。Asymptote 里最简单的读取数据的方法是读入空白分隔的文本文件，打开文件之后只要对一个数组或者矩阵进行赋值就可以读入一行或者一块数据：

import graph3;
import palette;
size3(150, IgnoreAspect);
// Open the data file
file in=input("data.txt").line();
// read file by assignment
// this read a line of numbers as an array
real[] x=in;  // first line
real[] y=in;  // second line
// read the rest of the file as a matrix
// 0, 0 means do not restrict the number of
// elements to read in either dimension
real[][] z=in.dimension(0,0);
triple f(pair t) {
  int i = round(t.x);
  int j = round(t.y);
  return (x[i], y[j], z[i][j]);
}

数据文件格式非常简单，头两行分别是两个参数 $x$ 和 $y$ 的值列表，然后剩下的行是整个数据矩阵 $z$ 的一个表格。通过 Numpy 的 savetxt 函数很容易导出。在 Asymptote 里读入数据之后我们就可以构造查表函数 $f$ 了，从上面可以看到 $f$ 只是直接通过下标取得相应的坐标而已。接下来就可以直接构造 surface 并进行绘制了：

surface s = surface(f, (0,0), (x.length-1, y.length-1), x.length-1, y.length-1);
s.colors(palette(s.map(zpart), Rainbow()));
draw(s, meshpen=blue);
triple m=currentpicture.userMin();
triple M=currentpicture.userMax();
triple target=0.5*(m+M);
currentprojection=perspective(camera=target+realmult(dir(60,210),M-m),
                              target=target);
xaxis3(Label("$\lambda_1$",position=MidPoint,align=-Y-Z),
       Bounds(),blue,OutTicks(Step=0.25,step=0.05));
       //Bounds(),blue,OutTicks(Label(align=-Y-X)));
yaxis3(Label("$\lambda_2$",position=MidPoint,align=-5X),
       Bounds(),red,OutTicks(Step=0.25,step=0.05));
zaxis3("Error",Bounds(),black,OutTicks(Step=0.25,step=0.05));

代码非常直接，唯一需要简单注意一下的是我们在调用 surface 函数的时候，传递了参数 (0,0) 和 (x.length-1, y.length-1)，这里对应 $f$ 在查表时的输入序列。

这样就大功告成了，当然缺点就是 Adobe 家族以外的 PDF 阅读器都看不了。第三个对于 viewer 来说比较 user friendly 的选项就是通过 web 页面。现在在 webGL 之类的技术支持下，其实 web 页面里渲染 3D 对象的效果其实已经非常好了。

比如之前在网上看到这个 3D 的卡通画，简直太惊艳了，我觉得现在的各种 3D 游戏之类的都处于严重的 Uncanny Valley 之中，让我非常难以接受，相反若是做成这种风格，应该会（让我觉得）赏心悦目很多。然而虽然看起来只是简单的 line drawing 的结果，但是实际的制作过程还是要进行正儿八经的三维建模、渲染之类的，作者在这里给了制作过程介绍，看起来似乎还是相当费力的。另外还有这里也有一些非常漂亮的 3D 线条漫画，看起来都非常酷，而且都是直接在浏览器了渲染出来的，不需要额外安装什么很复杂的 viewer 。

就我所知范围，目前的绘图工具中似乎 plotly 算是对 webgl 支持比较好并且也简单易用的。它们的 3D 图大概长下面这个样子，这里有一个在线的例子可以直接进行交互，渲染和交互效果都挺好的。

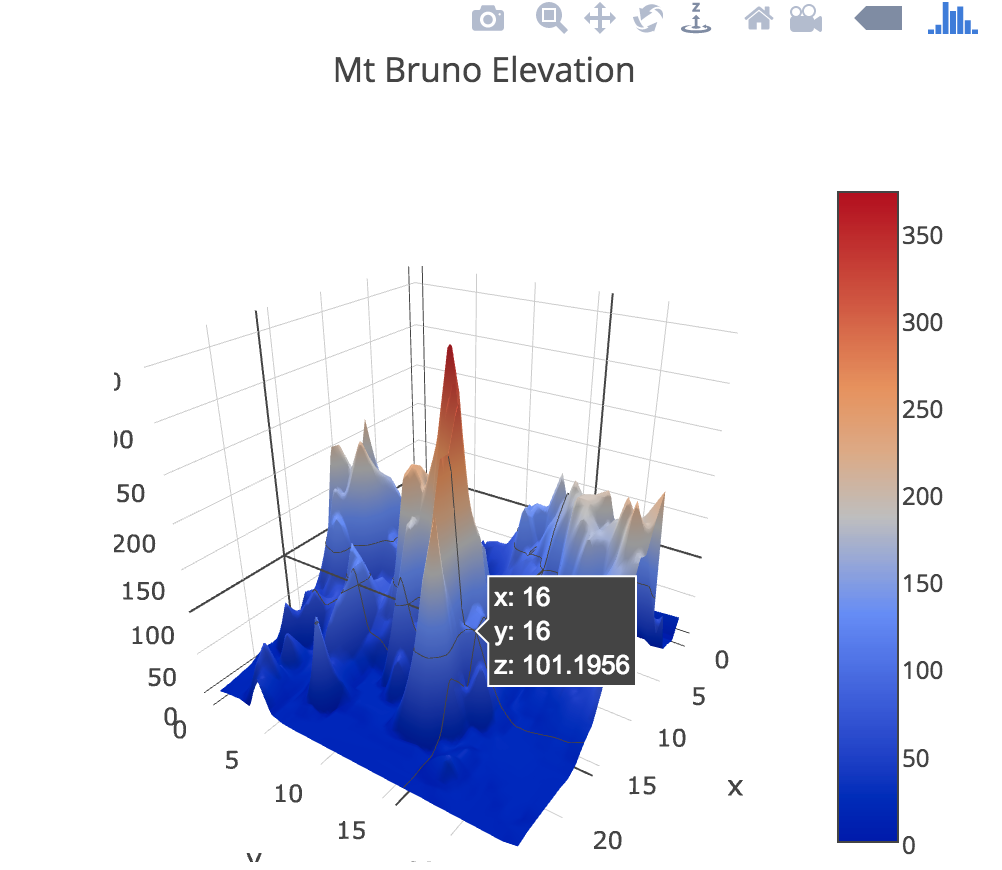
例如直接用我们刚才的 Python 里的数据的话，用下面的代码可以直接生成 plotly 的图，结果保持成一个 HTML 文件。文件里内嵌的 viewer，应该用任意一个现代一点的浏览器都能打开预览和交互。

import plotly
import plotly.graph_objs as go
data = [go.Surface(z=Z, x=XX, y=YY)]
layout = go.Layout(title='Test Plot', autosize=True)
fig = go.Figure(data=data, layout=layout)
# save offline standalone HTML files
plotly.offline.plot(fig, filename='test-plot')

唯一的缺点可能就是由于内嵌的 viewer，所以 HTML 文件还是比较大的，一个简单的 surface plot 大概也需要 2M 左右。另外 plotly 还能内嵌在 Jupyter Notebook 里预览交互图，它还提供收费的云服务可以在服务器上 host 你的 figure。

感觉以后的科技论文格式应该允许更多的交互内容，嵌入视频、音频、交互图表之类的，还有更全的 meta data，图表、公式、引用的预览、跳转等等。然而现实是目前很多地方还会要求 plot 必须是在黑白打印的情况下也能分辨的。