在之前讲
Projected Gradient Method 的文章 中,我们举了一个对加了白噪声的 Lena
的照片进行 denoising 的例子,文中提到了两种方法,一种是直接对 DWT
的系数进行 hard
thresholding,将数值较小的值设为零,再用逆向离散小波变换得到 denoising
之后的图片。另一种方法是解一个
ℓ 1 \ell_1 ℓ 1
当然,直观来讲,是不难理解的,因为 natural image
在小波基下呈现稀疏性,而白噪声,也就是 Gaussian
Noise,则没有稀疏性,另外假设 noise 的 scale
和原始信号相对来说比较小的话,那么通过 hard
thresholding,去掉那些较小的系数之后得到的稀疏系数会达到一定的降噪效果。我们在这里试图将问题
formally 定义出来。首先,我们假设 Lena 的图片是这样生成的
y = X w ∗ + ϵ (1)
y = Xw^* + \epsilon
\label{b16194a20d7d8f0d1a4e93f7b282324c1712bfb3}\tag{1}
y = X w ∗ + ϵ ( 1 )
其中
X ∈ R d × d X\in\mathbb{R}^{d\times d} X ∈ R d × d w ∗ ∈ R d w^*\in\mathbb{R}^d w ∗ ∈ R d ϵ ∼ N ( 0 , σ 2 I d ) \epsilon\sim \mathcal{N}(0, \sigma^2I_d) ϵ ∼ N ( 0 , σ 2 I d ) ϵ \epsilon ϵ σ 2 \sigma^2 σ 2
因此,我们所观测到的
y y y ϵ \epsilon ϵ X X X w ∗ w^* w ∗ w ^ \hat{w} w ^
M S E ( X w ^ ) = ∣ X w ∗ − X w ^ ∣ 2 2 (2)
\mathsf{MSE}(X\hat{w}) = |Xw^* - X\hat{w}|_2^2
\label{3dfc057e960580884decbffdc892c46944becdf7}\tag{2}
MSE ( X w ^ ) = ∣ X w ∗ − X w ^ ∣ 2 2 ( 2 )
注意 MSE 是一个随机变量,随机性来自
w ^ \hat{w} w ^ w ^ \hat{w} w ^ y y y y y y ϵ \epsilon ϵ X X X w ∗ w^* w ∗ y y y X X X w ∗ w^* w ∗ X w ^ X\hat{w} X w ^ X w ∗ Xw^* X w ∗
在构造 estimator
之前,我们先对问题进行一些简单的变换,首先注意到小波基是一个 orthonormal
basis,也就是说
X ⊤ X = I X^\top X=I X ⊤ X = I (eq:
1) 两边同时乘以
X ⊤ X^\top X ⊤
X ⊤ y = w ∗ + X ⊤ ϵ
X^\top y = w^* + X^\top \epsilon
X ⊤ y = w ∗ + X ⊤ ϵ
记
X ⊤ y = Y X^\top y=Y X ⊤ y = Y X ⊤ ϵ X^\top \epsilon X ⊤ ϵ ξ \xi ξ
Y = w ∗ + ξ (3)
Y = w^* + \xi
\label{0a06a34eecddabcdab7fd6cfdf7c8b2bdfe39c8a}\tag{3}
Y = w ∗ + ξ ( 3 )
其中
Y Y Y ξ \xi ξ X ⊤ X^\top X ⊤ ξ ∼ N ( 0 , σ 2 I d ) \xi \sim\mathcal{N}(0,\sigma^2 I_d) ξ ∼ N ( 0 , σ 2 I d )
M S E ( X w ^ ) = ( w ∗ − w ^ ) ⊤ X ⊤ X ( w ∗ − w ^ ) = ∣ w ∗ − w ^ ∣ 2 2
\begin{aligned}
\mathsf{MSE}(X\hat{w}) &= (w^*-\hat{w})^\top X^\top X (w^*-\hat{w})\\
&= |w^*-\hat{w}|_2^2
\end{aligned}
MSE ( X w ^ ) = ( w ∗ − w ^ ) ⊤ X ⊤ X ( w ∗ − w ^ ) = ∣ w ∗ − w ^ ∣ 2 2
现在问题变得简介了许多:我们观测到一个未知的向量
w ∗ w^* w ∗ w ∗ w^* w ∗ ℓ 2 \ell_2 ℓ 2 Y Y Y
接下来我们不妨来分析一下 Lena 和噪声各自的性质。首先 Lena 作为一张
natural image,在小波基下的系数
w ∗ w^* w ∗ Wikipedia ,一个高斯分布的随机变量取值在均值加减
3 σ 3\sigma 3 σ σ 2 \sigma^2 σ 2
根据这个,我们可以以很大的概率确定如下情况:
∣ ξ i ∣ |\xi_i| ∣ ξ i ∣ ∣ Y i ∣ |Y_i| ∣ Y i ∣ i i i ∣ w i ∗ ∣ ≠ 0 |w^*_i|\neq 0 ∣ w i ∗ ∣ = 0 ∣ Y i ∣ |Y_i| ∣ Y i ∣
w ^ HRD ( Y ) i = { Y i ∣ Y i ∣ > 2 τ 0 ∣ Y i ∣ ≤ 2 τ (4)
\hat{w}^{\text{HRD}}(Y)_i = \begin{cases}
Y_i & |Y_i| > 2\tau \\
0 & |Y_i| \leq 2\tau
\end{cases}
\label{b79b92176097564e295e9fcd719d514003ec9032}\tag{4}
w ^ HRD ( Y ) i = { Y i 0 ∣ Y i ∣ > 2 τ ∣ Y i ∣ ≤ 2 τ ( 4 )
这里的 threshold
2 τ 2\tau 2 τ ∣ Y i ∣ |Y_i| ∣ Y i ∣ ∣ Y i ∣ |Y_i| ∣ Y i ∣
接下来就让我们把这个 idea
具体地用数学语言描述出来。首先,让我们来具体刻画一下高斯分布的 tail
decay。具体来说,假设
Z Z Z σ 2 \sigma^2 σ 2 t > 0 t>0 t > 0 Z > t Z > t Z > t
P ( Z > t ) = ∫ t ∞ p Z ( z ) d z = ∫ t ∞ 1 2 π σ 2 e − z 2 / 2 σ 2 d z
\begin{aligned}
P(Z > t) &= \int_t^\infty p_Z(z)\,dz\\
&= \int_t^\infty \frac{1}{\sqrt{2\pi\sigma^2}}e^{-z^2/2\sigma^2}\,dz
\end{aligned}
P ( Z > t ) = ∫ t ∞ p Z ( z ) d z = ∫ t ∞ 2 π σ 2 1 e − z 2 /2 σ 2 d z
排除 Q-function
这种耍赖的存在的话,这个积分并没有一个表达式可以直接写出来,如果我们通过数值方法,可以算出类似刚才的
e σ e\sigma e σ t t t P ( Z > t ) P(Z > t) P ( Z > t ) z ≥ t z \geq t z ≥ t z / t ≥ 1 z/t \geq 1 z / t ≥ 1
∫ t ∞ 1 2 π σ 2 e − z 2 / 2 σ 2 d z ≤ ∫ t ∞ z t 1 2 π σ 2 e − z 2 / 2 σ 2 d z = σ 2 π t e − t 2 / 2 σ 2
\begin{aligned}
\int_t^\infty \frac{1}{\sqrt{2\pi\sigma^2}}e^{-z^2/2\sigma^2}\,dz &\leq
\int_t^\infty \frac{z}{t}\frac{1}{\sqrt{2\pi\sigma^2}}e^{-z^2/2\sigma^2}\,dz \\
&= \frac{\sigma}{\sqrt{2\pi}t}e^{-t^2/2\sigma^2}
\end{aligned}
∫ t ∞ 2 π σ 2 1 e − z 2 /2 σ 2 d z ≤ ∫ t ∞ t z 2 π σ 2 1 e − z 2 /2 σ 2 d z = 2 π t σ e − t 2 /2 σ 2
从这里可以看出,高斯分布的 tail 是以
e t 2 / 2 σ 2 e^{t^2/2\sigma^2} e t 2 /2 σ 2 t t t σ 2 \sigma^2 σ 2 σ / 2 π t \sigma/\sqrt{2\pi}t σ / 2 π t t t t t > 0 t>0 t > 0 P ( Z > t ) < 1 / 2 P(Z>t)<1/2 P ( Z > t ) < 1/2 Chernoff Bound
可以直接得到这样的方便处理的上界:
P ( Z > t ) ≤ e − t 2 / 2 σ 2
P(Z > t) \leq e^{-t^2/2\sigma^2}
P ( Z > t ) ≤ e − t 2 /2 σ 2
虽然推导并不复杂,但是篇幅有限,为了避免扯得太远,这里就直接使用这个结论了。现在我们回到
ξ \xi ξ d d d σ 2 I d \sigma^2I_d σ 2 I d
P ( ∣ ξ i ∣ > t ) ≤ P ( ξ i > t ) + P ( ξ i < − t ) ≤ 2 e − t 2 / 2 σ 2 (5)
P(|\xi_i| > t) \leq P(\xi_i > t) + P(\xi_i < -t) \leq 2e^{-t^2/2\sigma^2}
\label{42f1dd42266a2abb93ebae413fb6e9ad9f394a98}\tag{5}
P ( ∣ ξ i ∣ > t ) ≤ P ( ξ i > t ) + P ( ξ i < − t ) ≤ 2 e − t 2 /2 σ 2 ( 5 )
如果我们想要同时控制所有的
ξ i \xi_i ξ i
P ( max 1 ≤ i ≤ d ∣ ξ i ∣ > t ) = p ( ⋃ i = 1 d { ∣ ξ i ∣ > t } ) ≤ ∑ i = 1 d P ( ∣ ξ i ∣ > t ) ≤ 2 d e − t 2 / 2 σ 2 (6)
\begin{aligned}
P\left( \max_{1\leq i \leq d} |\xi_i| > t\right) &= p\left( \bigcup_{i=1}^d \left\{ |\xi_i| > t \right\} \right) \\
&\leq \sum_{i=1}^d P(|\xi_i| > t)\\
& \leq 2de^{-t^2/2\sigma^2}
\end{aligned}
\label{dd00a96c2f4ced03f36acacd338a6419e09e462d}\tag{6}
P ( 1 ≤ i ≤ d max ∣ ξ i ∣ > t ) = p ( i = 1 ⋃ d { ∣ ξ i ∣ > t } ) ≤ i = 1 ∑ d P ( ∣ ξ i ∣ > t ) ≤ 2 d e − t 2 /2 σ 2 ( 6 )
令右边的式子等于
δ \delta δ t t t δ > 0 \delta>0 δ > 0 1 − δ 1-\delta 1 − δ
max 1 ≤ i ≤ d ∣ ξ i ∣ ≤ σ 2 log ( 2 d / δ ) (7)
\max_{1\leq i \leq d}|\xi_i| \leq \sigma\sqrt{2\log(2d/\delta)}
\label{dabee5aac11ddfcd418f0ed484e46af03640b42f}\tag{7}
1 ≤ i ≤ d max ∣ ξ i ∣ ≤ σ 2 log ( 2 d / δ ) ( 7 )
也就是说,以很高的概率,我们可以将所有
∣ ξ i ∣ |\xi_i| ∣ ξ i ∣ σ \sigma σ 1 / δ 1/\delta 1/ δ d d d τ \tau τ
1
定理 1 . 假设模型满足
(eq:
3) ,那么令
τ = σ 2 log ( 2 d / δ )
\tau = \sigma\sqrt{2\log(2d/\delta)}
τ = σ 2 log ( 2 d / δ ) δ > 0 \delta>0 δ > 0 (eq:
4) 所定义的 Hard Threshold Estimator 可以以至少
1 − δ 1-\delta 1 − δ ∣ w ^ HRD − w ∗ ∣ 2 2 ≲ k σ 2 log ( 2 d / δ )
|\hat{w}^{\text{HRD}}-w^*|_2^2 \lesssim k\sigma^2 \log(2d/\delta)
∣ w ^ HRD − w ∗ ∣ 2 2 ≲ k σ 2 log ( 2 d / δ ) k = ∣ w ∗ ∣ 0 k=|w^*|_0 k = ∣ w ∗ ∣ 0 ∣ w i ∗ ∣ |w^*_i| ∣ w i ∗ ∣ 3 τ 3\tau 3 τ supp ( w ^ HRD ) = supp ( w ∗ )
\text{supp}(\hat{w}^{\text{HRD}}) = \text{supp}(w^*)
supp ( w ^ HRD ) = supp ( w ∗ )
这里
≲ \lesssim ≲ σ 2 \sigma^2 σ 2 σ \sigma σ 1 / d 1/d 1/ d k k k k k k w ∗ w^* w ∗ w ∗ w^* w ∗
w ^ = arg min w ∣ Y − w ∣ 2 2
\hat{w} = \operatorname*{\arg\min}_w |Y-w|_2^2
w ^ = w arg min ∣ Y − w ∣ 2 2
很显然最优解就是
w ^ = Y \hat{w}=Y w ^ = Y ∣ w ^ − w ∗ ∣ 2 2 = ∣ ξ ∣ 2 2 |\hat{w}-w^*|_2^2=|\xi|_2^2 ∣ w ^ − w ∗ ∣ 2 2 = ∣ ξ ∣ 2 2
P ( ∣ ξ ∣ 2 2 > t ) ≤ ∑ i = 1 d P ( ∣ ξ i ∣ 2 > t d ) ≤ ∑ i = 1 d P ( ∣ ξ i ∣ > t d ) ≤ 2 d exp ( − t 2 σ 2 d )
\begin{aligned}
P(|\xi|_2^2 > t) &\leq \sum_{i=1}^dP\left(|\xi_i|^2 > \frac{t}{d}\right)\\
&\leq \sum_{i=1}^dP\left(|\xi_i| > \sqrt{\frac{t}{d}}\right)\\
&\leq 2d\exp\left( -\frac{t}{2\sigma^2d} \right)
\end{aligned}
P ( ∣ ξ ∣ 2 2 > t ) ≤ i = 1 ∑ d P ( ∣ ξ i ∣ 2 > d t ) ≤ i = 1 ∑ d P ( ∣ ξ i ∣ > d t ) ≤ 2 d exp ( − 2 σ 2 d t )
令右边等于
δ \delta δ 1 − δ 1-\delta 1 − δ
∣ w ^ − w ∗ ∣ 2 2 ≤ 2 d σ 2 log ( 2 d / δ )
|\hat{w}-w^*|_2^2 \leq 2d\sigma^2 \log(2d/\delta)
∣ w ^ − w ∗ ∣ 2 2 ≤ 2 d σ 2 log ( 2 d / δ )
可以看到我们得到的 bound 和
w ^ HRD \hat{w}^{\text{HRD}} w ^ HRD d d d w ∗ w^* w ∗ k k k w ∗ w^* w ∗ k k k k k k w ^ HRD \hat{w}^{\text{HRD}} w ^ HRD k k k k k k
为方便起见,以下我们就记
w ^ HRD \hat{w}^{\text{HRD}} w ^ HRD w ^ \hat{w} w ^
∣ w ^ i − w i ∗ ∣ = ∣ w ^ i − w i ∗ ∣ 1 Y i > 2 τ + ∣ w ^ i − w i ∗ ∣ 1 Y i ≤ 2 τ = ∣ ξ i ∣ 1 Y i > 2 τ + ∣ w i ∗ ∣ 1 Y i ≤ 2 τ ≤ τ 1 Y i > 2 τ + ∣ w i ∗ ∣ 1 Y i ≤ 2 τ
\begin{aligned}
|\hat{w}_i-w^*_i| &= |\hat{w}_i-w^*_i|\mathbf{1}_{Y_i>2\tau} + |\hat{w}_i-w^*_i|\mathbf{1}_{Y_i\leq 2\tau} \\
&= |\xi_i|\mathbf{1}_{Y_i>2\tau} + |w^*_i|\mathbf{1}_{Y_i\leq 2\tau} \\
&\leq \tau \mathbf{1}_{Y_i>2\tau} + |w^*_i|\mathbf{1}_{Y_i\leq 2\tau}
\end{aligned}
∣ w ^ i − w i ∗ ∣ = ∣ w ^ i − w i ∗ ∣ 1 Y i > 2 τ + ∣ w ^ i − w i ∗ ∣ 1 Y i ≤ 2 τ = ∣ ξ i ∣ 1 Y i > 2 τ + ∣ w i ∗ ∣ 1 Y i ≤ 2 τ ≤ τ 1 Y i > 2 τ + ∣ w i ∗ ∣ 1 Y i ≤ 2 τ (eq:
7) ,是以至少
1 − δ 1-\delta 1 − δ τ \tau τ
∣ Y i ∣ > 2 τ ⇒ ∣ w i ∗ ∣ = ∣ Y i − ξ i ∣ ≥ ∣ Y i ∣ − ∣ ξ i ∣ > τ ∣ Y i ∣ ≤ 2 τ ⇒ ∣ w i ∗ ∣ = ∣ Y i − ξ i ∣ ≤ ∣ Y i ∣ + ∣ ξ i ∣ ≤ 3 τ
\begin{aligned}
|Y_i|>2\tau &\Rightarrow |w^*_i| = |Y_i - \xi_i| \geq |Y_i| - |\xi_i| > \tau \\
|Y_i|\leq 2\tau &\Rightarrow |w^*_i| = |Y_i-\xi_i| \leq |Y_i| + |\xi_i| \leq 3\tau
\end{aligned}
∣ Y i ∣ > 2 τ ∣ Y i ∣ ≤ 2 τ ⇒ ∣ w i ∗ ∣ = ∣ Y i − ξ i ∣ ≥ ∣ Y i ∣ − ∣ ξ i ∣ > τ ⇒ ∣ w i ∗ ∣ = ∣ Y i − ξ i ∣ ≤ ∣ Y i ∣ + ∣ ξ i ∣ ≤ 3 τ
因此,接着上面的不等式
∣ w ^ i − w i ∗ ∣ ≤ τ 1 ∣ w i ∗ ∣ > τ + ∣ w i ∗ ∣ 1 ∣ w i ∗ ∣ ≤ 3 τ
|\hat{w}_i-w^*_i| \leq \tau \mathbf{1}_{|w^*_i|>\tau} + |w^*_i|\mathbf{1}_{|w^*_i|\leq 3\tau}
∣ w ^ i − w i ∗ ∣ ≤ τ 1 ∣ w i ∗ ∣ > τ + ∣ w i ∗ ∣ 1 ∣ w i ∗ ∣ ≤ 3 τ
我们将右边的式子分情况展开可以得到
τ 1 ∣ w i ∗ ∣ > τ + ∣ w i ∗ ∣ 1 ∣ w i ∗ ∣ ≤ 3 τ = { τ + ∣ w i ∗ ∣ τ < ∣ w i ∗ ∣ ≤ 3 τ ∣ w i ∗ ∣ ∣ w i ∗ ∣ ≤ τ τ ∣ w i ∗ ∣ > 3 τ ≤ { 4 τ τ < ∣ w i ∗ ∣ ≤ 3 τ ∣ w i ∗ ∣ ∣ w i ∗ ∣ ≤ τ τ ∣ w i ∗ ∣ > 3 τ ≤ { 4 τ τ < ∣ w i ∗ ∣ ∣ w i ∗ ∣ ∣ w i ∗ ∣ ≤ τ ≤ { 4 τ τ < ∣ w i ∗ ∣ 4 ∣ w i ∗ ∣ ∣ w i ∗ ∣ ≤ τ
\begin{aligned}
\tau \mathbf{1}_{|w^*_i|>\tau} + |w^*_i|\mathbf{1}_{|w^*_i|\leq 3\tau}
&= \begin{cases}
\tau + |w_i^*| & \tau<|w_i^*|\leq 3\tau \\
|w^*_i| & |w^*_i| \leq \tau \\
\tau & |w^*_i| > 3\tau
\end{cases}\\
& \leq \begin{cases}
4\tau & \tau<|w_i^*|\leq 3\tau \\
|w^*_i| & |w^*_i| \leq \tau \\
\tau & |w^*_i| > 3\tau
\end{cases}\\
& \leq \begin{cases}
4\tau & \tau<|w_i^*|\\
|w^*_i| & |w^*_i| \leq \tau \\
\end{cases}\\
& \leq \begin{cases}
4\tau & \tau<|w_i^*|\\
4|w^*_i| & |w^*_i| \leq \tau \\
\end{cases}
\end{aligned}
τ 1 ∣ w i ∗ ∣ > τ + ∣ w i ∗ ∣ 1 ∣ w i ∗ ∣ ≤ 3 τ = ⎩ ⎨ ⎧ τ + ∣ w i ∗ ∣ ∣ w i ∗ ∣ τ τ < ∣ w i ∗ ∣ ≤ 3 τ ∣ w i ∗ ∣ ≤ τ ∣ w i ∗ ∣ > 3 τ ≤ ⎩ ⎨ ⎧ 4 τ ∣ w i ∗ ∣ τ τ < ∣ w i ∗ ∣ ≤ 3 τ ∣ w i ∗ ∣ ≤ τ ∣ w i ∗ ∣ > 3 τ ≤ { 4 τ ∣ w i ∗ ∣ τ < ∣ w i ∗ ∣ ∣ w i ∗ ∣ ≤ τ ≤ { 4 τ 4∣ w i ∗ ∣ τ < ∣ w i ∗ ∣ ∣ w i ∗ ∣ ≤ τ
也就是说
∣ w ^ i − w i ∗ ∣ ≤ 4 min ( τ , ∣ w i ∗ ∣ )
|\hat{w}_i-w^*_i| \leq 4\min(\tau, |w^*_i|)
∣ w ^ i − w i ∗ ∣ ≤ 4 min ( τ , ∣ w i ∗ ∣ )
从而,我们可以直接得到
∣ w ^ − w ∗ ∣ 2 2 = ∑ i = 1 d ∣ w ^ i − w i ∗ ∣ 2 ≤ 16 ∑ i = 1 d ( min ( τ , ∣ w i ∗ ∣ ) ) 2 ≤ 16 ∣ w i ∗ ∣ 0 τ 2
\begin{aligned}
|\hat{w}-w^*|_2^2 &= \sum_{i=1}^d |\hat{w}_i-w^*_i|^2 \\
&\leq 16\sum_{i=1}^d \left(\min(\tau, |w^*_i|)\right)^2 \\
&\leq 16|w^*_i|_0\tau^2
\end{aligned}
∣ w ^ − w ∗ ∣ 2 2 = i = 1 ∑ d ∣ w ^ i − w i ∗ ∣ 2 ≤ 16 i = 1 ∑ d ( min ( τ , ∣ w i ∗ ∣ ) ) 2 ≤ 16∣ w i ∗ ∣ 0 τ 2
带入定理中
τ \tau τ w i ∗ ≠ 0 w^*_i\neq 0 w i ∗ = 0 ∣ w i ∗ ∣ > 3 τ |w^*_i|>3\tau ∣ w i ∗ ∣ > 3 τ
∣ Y i ∣ = ∣ w i ∗ + ξ i ∣ ≥ ∣ w i ∗ ∣ − ∣ ξ i ∣ > 2 τ
|Y_i| = |w^*_i + \xi_i| \geq |w^*_i| - |\xi_i| > 2\tau
∣ Y i ∣ = ∣ w i ∗ + ξ i ∣ ≥ ∣ w i ∗ ∣ − ∣ ξ i ∣ > 2 τ
于是
supp ( w ∗ ) ⊂ supp ( w ^ ) \text{supp}(w^*)\subset\text{supp}(\hat{w}) supp ( w ∗ ) ⊂ supp ( w ^ ) ∣ Y i ∣ > 2 τ |Y_i|>2\tau ∣ Y i ∣ > 2 τ
∣ w i ∗ ∣ = ∣ Y i − ξ i ∣ ≥ ∣ Y i ∣ − ∣ ξ i ∣ > τ > 0
|w^*_i| = |Y_i-\xi_i| \geq |Y_i| -|\xi_i| > \tau > 0
∣ w i ∗ ∣ = ∣ Y i − ξ i ∣ ≥ ∣ Y i ∣ − ∣ ξ i ∣ > τ > 0
于是
supp ( w ^ ) ⊂ supp ( w ∗ ) \text{supp}(\hat{w})\subset\text{supp}(w^*) supp ( w ^ ) ⊂ supp ( w ∗ )
结束之前,有几点注意事项。除了上面的 hard thresholding
之外,还可以定义 soft thresholding,也就是先对所有的系数的绝对值减去
2 τ 2\tau 2 τ X X X X X X w ∗ w^* w ∗ X X X X w ∗ = 0 Xw^*=0 X w ∗ = 0 X X X X X X X X X w ∗ w^* w ∗ d d d k k k n n n n n n
最后,理论分析里得到的
τ \tau τ
由于本文没有什么图片,看起来比较枯燥,下面随便给了一段用来通过 hard
thresholding 和 soft thresholding 对 Lena 的图片进行去噪的 julia
代码。
# Requires the following packages: # # Pkg.add("Wavelets") # Pkg.add("Images") using Images using Wavelets sigma = 0.1 dim = 512 * 512 delta = 0.1 img = reinterpret ( Float64 , float64 ( imread ( "lena512gray.bmp" ))) imwrite ( img , "threshold-lena-orig.jpg" ) # add noise to the image img . data += 0.2 * randn ( size ( img . data )) imwrite ( img , "threshold-lena-noisy.jpg" ) the_wavelet = wavelet ( WT . sym4 ) img_coef = dwt ( img . data , the_wavelet ) for config in [ "bound" , "choose" ] if config == "bound" tau = sigma * sqrt ( 2 * log ( 2 * dim / delta )) else tau = 0.25 end # hard thresholding img_coef_hrd = copy ( img_coef ) img_coef_hrd [ abs ( img_coef_hrd ) .<= 2 tau ] = 0 rcv_img = idwt ( img_coef_hrd , the_wavelet ) imwrite ( rcv_img ' , "threshold-lena-hrd- $config -rcv.jpg" ) # soft thresholding if config == "choose" tau = 0.1 end img_coef_sft = copy ( img_coef ) coef = 1 - 2 tau ./ abs ( img_coef_sft ) coef = coef .* ( coef .> 0 ) img_coef_sft = img_coef_sft .* coef rcv_img = idwt ( img_coef_sft , the_wavelet ) imwrite ( rcv_img ' , "threshold-lena-sft- $config -rcv.jpg" ) end
我们对比了 hard thresholding 和 soft thresholding 使用定理中给定的
τ \tau τ τ \tau τ
可以看到,定理中给出的
τ \tau τ

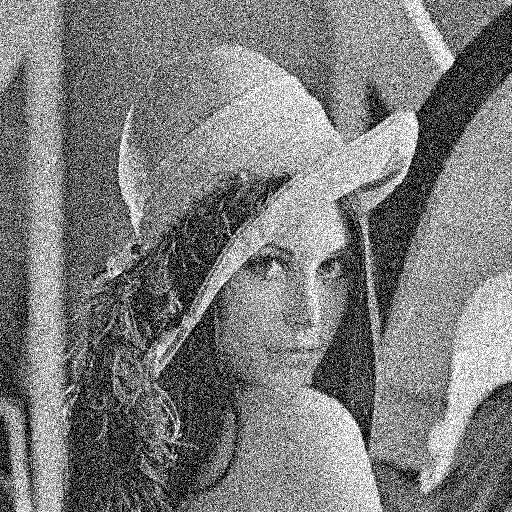




如果基于 Disqus 的评论系统无法加载,可以使用下面基于 Github 的评论系统(需要使用 Github 账号登陆)。