CS,全称一般被认为是 Compressive/Compressed
Sensing/Sampling,中文叫做压缩感知,于 2004 至 2006 年之间由 David
Donoho、Emamnuel Candes、Terry Tao
等人提出来之后,迅速发展壮大,虽然里组成 CS
理论的基本元素往前追溯都都有很多前人的研究,但是也是在把整个东西系统地提出来了之后,才引发了后续的广泛关注,从纯理论到纯应用甚至是新硬件的构造等等各方面。而
CS 本身也是认为是信号处理领域自 Shannon/Nyquist
采样理论以来的重大突破。
因为 Shannon/Nyquist 采样理论使得我们可以用离散信号去 perfectly
重构原来的(如果是 band-limited
并且采样率足够高的话)连续信号,而离散时间信号处理借助于计算机的力量使得人们可以实现现在的各种复杂的信号处理和滤波,如果我们还在用
Analog 设备直接对 Analog
信号进行各种处理的话,这些东西估计都难以想象吧。然而有些问题里的信号并不是完全
band-limited 的,或者要求的 Nyquist
频率过高使得硬件限制等各种原因无法完成有效地采样,然后压缩感知的理论跳出来说,如果信号在某个已知的 基下面是稀疏的的话,我们可以使用远低于
Nyquist
频率的代价来完成采样并完美地恢复出原始信号,与此同时,在实际应用中的各种信号,由于具有其各自的结构性,所以通常在合适的
basic 或者 dictionary
下面都会表现出稀疏性(例如自然景观图像在小波域下是稀疏的),另外,Machine
Learning 还专门有一个 topic 叫做 sparse
learning,其重要的一个目标就是给定一个数据集,构造一个 dictionary
使得该数据集在这个 dictionary
下具有稀疏的线性表达。所以压缩感知的提出被认为是又一次重大革命。
当然把 CS 和 Shannon/Nyquist
采样理论直接并列起来比较的话,还是有一些设定不一样的地方,比如经典的采样理论一般讨论的需要采样的信号是连续时间的,无穷维的信号,而
CS
中虽然也有扩展理论尝试处理无穷维的信号,但是主要的着眼点还是在于长度为
N N N
具体来说,CS 着眼于一个
N N N x x x N N N a i a_i a i y i = ⟨ a i , x ⟩ y_i=\langle a_i, x\rangle y i = ⟨ a i , x ⟩ n n n n × N n\times N n × N A A A A A A y = A x y=Ax y = A x x x x
线性代数的知识告诉我们,如果
n < N n<N n < N A A A N N N x 0 x_0 x 0
x ′ = x 0 + x ˉ , x ˉ ∈ N
x' = x_0 + \bar{x},\quad \bar{x}\in\mathcal{N}
x ′ = x 0 + x ˉ , x ˉ ∈ N
都是该问题的解,其中
N = { x ˉ : A x ˉ = 0 }
\mathcal{N}=\{\bar{x}: A\bar{x} = 0\}
N = { x ˉ : A x ˉ = 0 }
是矩阵
A A A x x x A A A x x x k k k ∥ x ∥ 0 ≤ k \|x\|_0\leq k ∥ x ∥ 0 ≤ k k k k k k k Σ k \Sigma_k Σ k Σ k ⊂ Σ k + 1 \Sigma_k\subset\Sigma_{k+1} Σ k ⊂ Σ k + 1
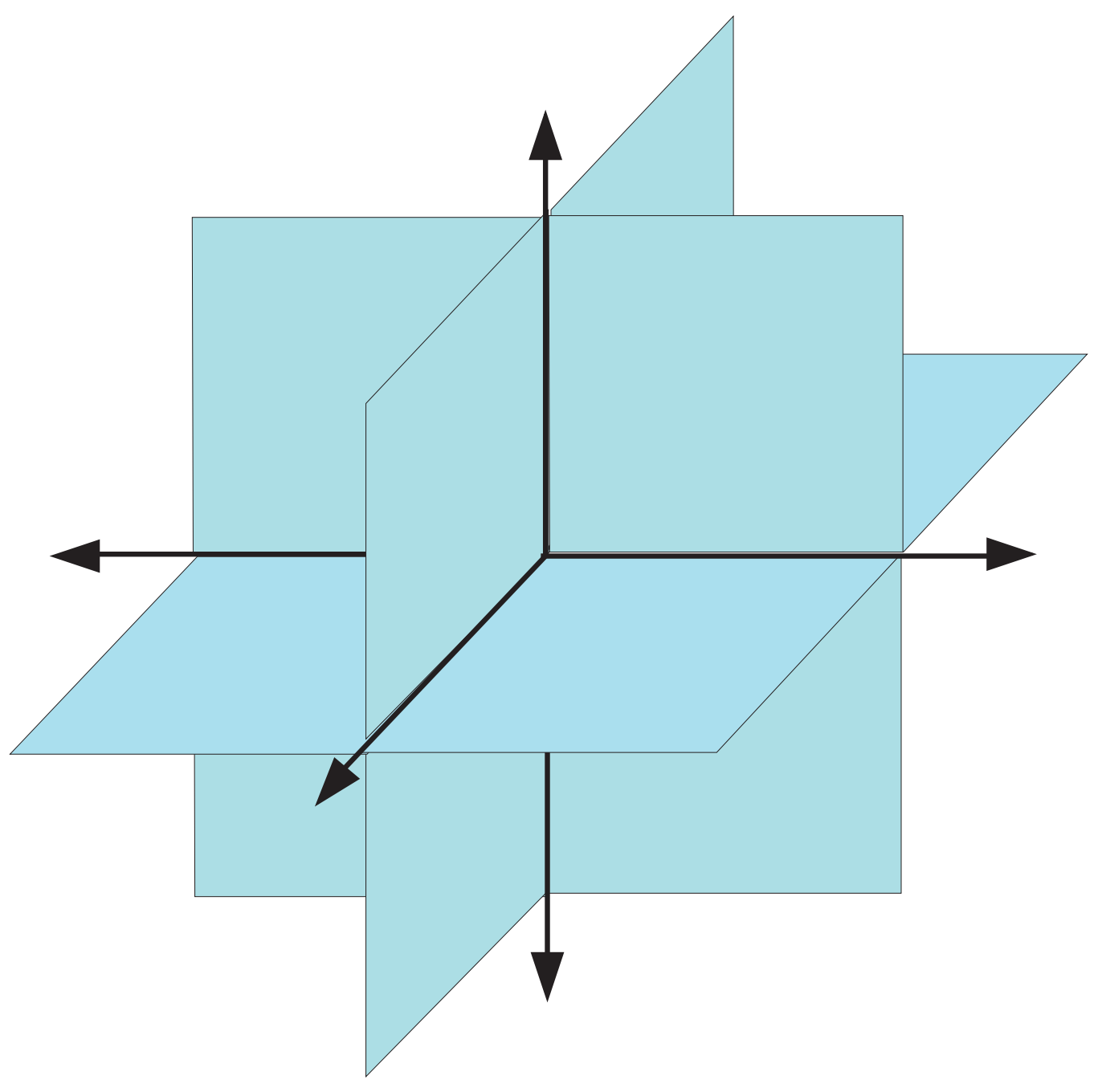
直观来说,Σ k \Sigma_k Σ k ( N k ) \binom{N}{k} ( k N ) k k k k k k R 3 \mathbb{R}^3 R 3 Σ 2 \Sigma_2 Σ 2 (img:
1) 所示。
如果我们已知了
x x x k k k N ∩ Σ 2 k = { 0 } \mathcal{N}\cap \Sigma_{2k}=\{0\} N ∩ Σ 2 k = { 0 } x 1 x_1 x 1 x 2 x_2 x 2
A ( x 1 − x 2 ) = A x 1 − A x 2 = y − y = 0
A(x_1-x_2) = Ax_1 - Ax_2 = y - y = 0
A ( x 1 − x 2 ) = A x 1 − A x 2 = y − y = 0
换句话说,x 1 − x 2 ∈ N x_1-x_2\in \mathcal{N} x 1 − x 2 ∈ N x 1 x_1 x 1 x 2 x_2 x 2 k k k x 1 − x 2 ∈ Σ 2 k x_1-x_2\in\Sigma_{2k} x 1 − x 2 ∈ Σ 2 k Σ 2 k \Sigma_{2k} Σ 2 k N \mathcal{N} N x 1 − x 2 = 0 x_1-x_2=0 x 1 − x 2 = 0
为了更方便地描述这种情况,人们模仿矩阵的 rank 构造出一个叫做 spark
的量,一个矩阵
A A A k k k A A A 存在
k k k k k k 所有
k + 1 k+1 k + 1 spark ( A ) > 2 k \text{spark}(A)>2k spark ( A ) > 2 k A A A Σ 2 k \Sigma_{2k} Σ 2 k
也就是说,如果我们已知原始的信号是
k k k 2 k 2k 2 k A A A
A A A Restricted
Isometry Property (RIP) , Coherence 之类的。构造具体的算法去进行
Decoding,这里通常分为三类:ℓ 1 \ell_1 ℓ 1
如何去验证一个给定的
A A A A A A ;p) 满足给定的性质。
于是再回到刚才关于 Null Space 的讨论中,虽然 Spark 的条件给出了在
x ∈ Σ k x\in\Sigma_k x ∈ Σ k k k k k k k k k k
σ k ( x ) X = min z ∈ Σ k ∥ x − z ∥ X
\sigma_k(x)_X = \min_{z\in\Sigma_k}\|x-z\|_X
σ k ( x ) X = z ∈ Σ k min ∥ x − z ∥ X
当然,如果
x x x k k k ∥ ⋅ ∥ X \|\cdot\|_X ∥ ⋅ ∥ X ℓ p \ell_p ℓ p x x x k k k k k k (fig:
1) 以最近的一幅合作水彩作为例子,可以看到在 Wavelet
系数域里,只要保留 5%
那么多非零系数已经可以达到相当令人眼满意的近似结果。
回到 CS 的问题,在
x x x k k k x x x k k k
∥ x − Δ ( A x ) ∥ X ≤ C 0 σ k ( x ) X (1)
\|x-\Delta(A x)\|_X \leq C_0 \sigma_k(x)_X
\label{25c95221d2ba2dfa343638b1b0b578404c184ee6}\tag{1}
∥ x − Δ ( A x ) ∥ X ≤ C 0 σ k ( x ) X ( 1 )
其中
Δ \Delta Δ (fig:
1)
中的近似结果,这是我们在看到完整的原图之后,把所有的系数从大到小排序然后只保留前
k k k A A A n n n x x x k k k σ k ( x ) X = 0 \sigma_k(x)_X=0 σ k ( x ) X = 0
和之前一样,为了能够达到
(eq:
1) 中的目标,我们从
A A A A A A h ∈ N h\in\mathcal{N} h ∈ N
∥ h ∥ X ≤ C 0 σ 2 k ( h ) X (2)
\|h\|_X \leq C_0 \sigma_{2k}(h)_X
\label{bd57b00b7d41c31dc22bec44c1fdc0a158e7a461}\tag{2}
∥ h ∥ X ≤ C 0 σ 2 k ( h ) X ( 2 )
这个不等式直观上来说,就是在说
A A A N \mathcal{N} N h h h 2 k 2k 2 k h h h 2 k 2k 2 k (eq:
2) 右边将会等于零,于是左边也必须等于零,所以和之前一样,严格
2 k 2k 2 k 2 k 2k 2 k C 0 C_0 C 0 (eq:
1) 中对应起来的同一个常数)。
为了证明这一点,我们注意到对于任意的
h ∈ N h\in\mathcal{N} h ∈ N h = h 1 + h 2 + h 3 h=h_1+h_2+h_3 h = h 1 + h 2 + h 3 h 1 h_1 h 1 k k k h 2 h_2 h 2 k k k h 3 = h − h 1 − h 2 h_3=h-h_1-h_2 h 3 = h − h 1 − h 2 − h 1 ∈ Σ k -h_1\in\Sigma_k − h 1 ∈ Σ k (eq:
1) 我们可以保证无损重建,也就是说
− h 1 = Δ ( A ( − h 1 ) ) -h_1 = \Delta(A(-h_1)) − h 1 = Δ ( A ( − h 1 )) h ∈ N h\in\mathcal{N} h ∈ N
0 = A h = A ( h 1 + h 2 + h 3 ) ⇒ A ( h 2 + h 3 ) = A ( − h 1 )
0 = Ah = A(h_1 + h_2 + h_3)\quad\Rightarrow\quad A(h_2+h_3) = A(-h_1)
0 = A h = A ( h 1 + h 2 + h 3 ) ⇒ A ( h 2 + h 3 ) = A ( − h 1 )
因此同样地,我们有
− h 1 = Δ ( A ( h 2 + h 3 ) ) -h_1 = \Delta(A(h_2+h_3)) − h 1 = Δ ( A ( h 2 + h 3 ))
∥ h ∥ X = ∥ h 2 + h 3 − Δ ( A ( h 2 + h 3 ) ) ∥ X ≤ C 0 σ k ( h 2 + h 3 ) ≤ C 0 ∥ h 3 ∥ X = C 0 σ 2 k ( h )
\begin{aligned}
\|h\|_X &= \|h_2+h_3 - \Delta(A(h_2+h_3))\|_X \\
&\leq C_0\sigma_k(h_2+h_3) \\
&\leq C_0\|h_3\|_X \\
&= C_0\sigma_{2k}(h)
\end{aligned}
∥ h ∥ X = ∥ h 2 + h 3 − Δ ( A ( h 2 + h 3 )) ∥ X ≤ C 0 σ k ( h 2 + h 3 ) ≤ C 0 ∥ h 3 ∥ X = C 0 σ 2 k ( h )
即证。也就是说,为了实现
(eq:
1) ,必要条件是
A A A (eq:
2) ,该性质又被称为 Null Space Property
(NSP) 。实际上,通过改变一下常数,我们可以证明该条件同时是充分条件。具体来说,如果
∥ h ∥ X ≤ C 0 2 σ 2 k ( h ) X , ∀ h ∈ N (3)
\|h\|_X\leq \frac{C_0}{2}\sigma_{2k}(h)_X, \quad \forall h\in\mathcal{N}
\label{6b34eab95966ec74518ca926454607979fdd229f}\tag{3}
∥ h ∥ X ≤ 2 C 0 σ 2 k ( h ) X , ∀ h ∈ N ( 3 )
那么我们可以令 decoder 为
Δ ( y ) = arg min A z = y σ k ( z ) X
\Delta(y) = \operatorname*{arg\,min}_{Az = y}\sigma_k(z)_X
Δ ( y ) = A z = y arg min σ k ( z ) X
则,由 decoder
的定义知道,x − Δ ( A x ) x-\Delta(Ax) x − Δ ( A x ) (eq:
3) ,我们有
∥ x − Δ ( A x ) ∥ X ≤ C 0 2 σ 2 k ( x − Δ ( A x ) ) X ≤ C 0 2 ( σ k ( x ) X + σ k ( Δ ( A x ) ) X ) ≤ C 0 σ k ( x ) X
\begin{aligned}
\|x - \Delta(Ax)\|_X &\leq \frac{C_0}{2}\sigma_{2k}(x-\Delta(Ax))_X \\
&\leq \frac{C_0}{2}\left( \sigma_k(x)_X + \sigma_k(\Delta(Ax))_X \right) \\
&\leq C_0\sigma_k(x)_X
\end{aligned}
∥ x − Δ ( A x ) ∥ X ≤ 2 C 0 σ 2 k ( x − Δ ( A x ) ) X ≤ 2 C 0 ( σ k ( x ) X + σ k ( Δ ( A x ) ) X ) ≤ C 0 σ k ( x ) X
即证。其中最后一个不等式是由于我们所定义的 decoder 是对其参数的
σ k ( ⋅ ) X \sigma_k(\cdot)_X σ k ( ⋅ ) X ℓ 1 \ell_1 ℓ 1
需要注意的是,我们上面的结论其实并没有明确地要求
x x x k k k x x x (eq:
1) 右边本身就很大的话,这个 bound
就没有任何意义了。不过接下来我们还要再将我们的目标扩充一下:将测量误差考虑进来。换句话说,现在我们的
sample 结果将是
y = A x + e
y = Ax + e
y = A x + e
其中
e e e k k k x ∈ Σ k x\in\Sigma_k x ∈ Σ k
∥ Δ ( A x + e ) − x ∥ 2 ≤ C ∥ e ∥ 2
\|\Delta(Ax+e) - x\|_2 \leq C \|e\|_2
∥Δ ( A x + e ) − x ∥ 2 ≤ C ∥ e ∥ 2
为了达到这个 stable 的要求,我们必须要有,对任意的
x ∈ Σ 2 k x\in\Sigma_{2k} x ∈ Σ 2 k
1 C ∥ x ∥ 2 ≤ ∥ A x ∥ 2 (4)
\frac{1}{C}\|x\|_2 \leq \|Ax\|_2
\label{c15050c56f4fcae5497334d62a94f987f382659e}\tag{4}
C 1 ∥ x ∥ 2 ≤ ∥ A x ∥ 2 ( 4 )
为了证明这一必要条件,我们将
x x x x = x 1 − x 2 x=x_1-x_2 x = x 1 − x 2 x 1 , x 2 ∈ Σ k x_1,x_2\in\Sigma_k x 1 , x 2 ∈ Σ k
e 1 = A ( x 2 − x 1 ) 2 , e 2 = A ( x 1 − x 2 ) 2
e_1 = \frac{A(x_2-x_1)}{2},\quad e_2 = \frac{A(x_1-x_2)}{2}
e 1 = 2 A ( x 2 − x 1 ) , e 2 = 2 A ( x 1 − x 2 )
则
A x 1 + e 1 = A x 2 + e 2 = A ( x 1 + x 2 ) 2
Ax_1 + e_1 = Ax_2 + e_2 = \frac{A(x_1+x_2)}{2}
A x 1 + e 1 = A x 2 + e 2 = 2 A ( x 1 + x 2 )
记
x ^ = Δ ( A x 1 + e 1 ) = Δ ( A x 2 + e 2 ) \hat{x}=\Delta(Ax_1+e_1)=\Delta(Ax_2+e_2) x ^ = Δ ( A x 1 + e 1 ) = Δ ( A x 2 + e 2 )
∥ x ∥ 2 = ∥ x 1 − x 2 ∥ 2 = ∥ x 1 − x ^ + x ^ − x 2 ∥ 2 ≤ ∥ x 1 − x ^ ∥ 2 + ∥ x ^ − x 2 ∥ 2 ≤ C ∥ e 1 ∥ 2 + C ∥ e 2 ∥ 2 = C ∥ A ( x 1 − x 2 ) ∥ 2 = C ∥ A x ∥ 2
\begin{aligned}
\|x\|_2 &= \|x_1-x_2\|_2 \\
&= \|x_1-\hat{x} + \hat{x}-x_2\|_2 \\
&\leq \|x_1-\hat{x}\|_2 + \|\hat{x}-x_2\|_2 \\
&\leq C\|e_1\|_2 + C\|e_2\|_2 \\
&= C\|A(x_1-x_2)\|_2 \\
&= C\|Ax\|_2
\end{aligned}
∥ x ∥ 2 = ∥ x 1 − x 2 ∥ 2 = ∥ x 1 − x ^ + x ^ − x 2 ∥ 2 ≤ ∥ x 1 − x ^ ∥ 2 + ∥ x ^ − x 2 ∥ 2 ≤ C ∥ e 1 ∥ 2 + C ∥ e 2 ∥ 2 = C ∥ A ( x 1 − x 2 ) ∥ 2 = C ∥ A x ∥ 2
但是如果仅仅是
(eq:
4) 的话,我们可以仅仅通过对
A A A C C C (eq:
4) 的右边也进行一下限制。于是有了下面这个性质。
1
定义 1 (Restricted Isometry
Property (RIP)) . 对于矩阵
A A A δ k ∈ ( 0 , 1 ) \delta_k\in(0,1) δ k ∈ ( 0 , 1 ) x ∈ Σ k x\in\Sigma_k x ∈ Σ k ( 1 − δ k ) ∥ x ∥ 2 2 ≤ ∥ A x ∥ 2 2 ≤ ( 1 + δ k ) ∥ x ∥ 2 2
(1-\delta_k)\|x\|_2^2 \leq \|Ax\|_2^2 \leq (1+\delta_k)\|x\|_2^2
( 1 − δ k ) ∥ x ∥ 2 2 ≤ ∥ A x ∥ 2 2 ≤ ( 1 + δ k ) ∥ x ∥ 2 2 A A A k k k
这是一个比之前更强的性质,由
δ ∈ ( 0 , 1 ) \delta \in (0,1) δ ∈ ( 0 , 1 ) A A A k k k A A A k k k x ∈ Σ k x\in\Sigma_k x ∈ Σ k
0 = ∥ 0 ∥ 2 2 = ∥ A x ∥ 2 2 ≥ ( 1 − δ k ) ∥ x ∥ 2 2 > 0
0 = \|0\|_2^2 = \|Ax\|_2^2 \geq (1-\delta_k)\|x\|_2^2 > 0
0 = ∥0 ∥ 2 2 = ∥ A x ∥ 2 2 ≥ ( 1 − δ k ) ∥ x ∥ 2 2 > 0
除此之外,RIP 也比 NSP
要强。具体来说,我们有如下的定理。简单起见,在接下来的讨论中,我们将 NSP
限制为
∥ ⋅ ∥ X \|\cdot\|_X ∥ ⋅ ∥ X ℓ 1 \ell_1 ℓ 1
1
定理 1 . 如果
A A A 2 k 2k 2 k δ 2 k < 1 / 3 \delta_{2k}<1/3 δ 2 k < 1/3 A A A 2 k 2k 2 k
C 0 = 1 − δ 2 k 1 − 3 δ 2 k
C_0 = \frac{1-\delta_{2k}}{1-3\delta_{2k}}
C 0 = 1 − 3 δ 2 k 1 − δ 2 k
令
T 0 ⊂ { 1 , … , N } T_0\subset\{1,\ldots,N\} T 0 ⊂ { 1 , … , N } h h h k k k T 1 T_1 T 1 T 0 T_0 T 0 k k k T = T 0 ∪ T 1 T=T_0\cup T_1 T = T 0 ∪ T 1
σ 2 k ( h ) 1 = ∥ h T c ∥ 1
\sigma_{2k}(h)_1 = \|h_{T^c}\|_1
σ 2 k ( h ) 1 = ∥ h T c ∥ 1
接下来我们先证明对于
h ∈ N h\in \mathcal{N} h ∈ N
∥ h T ∥ 1 ≤ C ~ ∥ h T c ∥ 1
\|h_T\|_1 \leq \tilde{C}\|h_{T^c}\|_1
∥ h T ∥ 1 ≤ C ~ ∥ h T c ∥ 1
于是
∥ h ∥ 1 = ∥ h T ∥ 1 + ∥ h T c ∥ 1 ≤ ( 1 + C ~ ) ∥ h T c ∥ 1 ≜ C 0 ∥ h T c ∥ 1 (5)
\|h\|_1 = \|h_T\|_1 + \|h_{T^c}\|_1 \leq (1+\tilde{C})\|h_{T^c}\|_1\triangleq C_0\|h_{T^c}\|_1
\label{6e22ac41d7058bfa493e8f8fe3127633d4290918}\tag{5}
∥ h ∥ 1 = ∥ h T ∥ 1 + ∥ h T c ∥ 1 ≤ ( 1 + C ~ ) ∥ h T c ∥ 1 ≜ C 0 ∥ h T c ∥ 1 ( 5 )
在证明中我们还需有用到如下的引理。
1
引理 1 . 若
A A A 2 k 2k 2 k h h h A A A T 0 , T 1 , T 2 , … T_0,T_1,T_2,\ldots T 0 , T 1 , T 2 , … T = T 0 ∪ T 1 T=T_0\cup T_1 T = T 0 ∪ T 1
∥ h T ∥ 2 ≤ α ∥ h T 0 c ∥ 1 k
\|h_T\|_2 \leq \alpha \frac{\|h_{T_0^c}\|_1}{\sqrt{k}}
∥ h T ∥ 2 ≤ α k ∥ h T 0 c ∥ 1
其中
α = 2 δ 2 k 1 − δ 2 k
\alpha = \frac{\sqrt{2}\delta_{2k}}{1-\delta_{2k}}
α = 1 − δ 2 k 2 δ 2 k
引理(的更 general 的情况,不要求
h h h Compressive
Sensing: Theory and Applications 》第一章中的引理
1.3。继续我们定理的证明,根据引理,我们有
∥ h T ∥ 1 ≤ 2 k ∥ h T ∥ 2 ≤ 2 α ∥ h T 0 c ∥ 1 = 2 α ( ∥ h T c ∥ 1 + ∥ h T 1 ∥ 1 ) ≤ 2 α ( ∥ h T c ∥ 1 + ∥ h T ∥ 1 )
\begin{aligned}
\|h_T\|_1 &\leq \sqrt{2k}\|h_T\|_2 \\
&\leq \sqrt{2}\alpha\|h_{T_0^c}\|_1 \\
&= \sqrt{2}\alpha \left( \|h_{T^c}\|_1 + \|h_{T_1}\|_1 \right) \\
&\leq \sqrt{2}\alpha \left( \|h_{T^c}\|_1 + \|h_T\|_1 \right)
\end{aligned}
∥ h T ∥ 1 ≤ 2 k ∥ h T ∥ 2 ≤ 2 α ∥ h T 0 c ∥ 1 = 2 α ( ∥ h T c ∥ 1 + ∥ h T 1 ∥ 1 ) ≤ 2 α ( ∥ h T c ∥ 1 + ∥ h T ∥ 1 )
整理得
( 1 − 2 α ) ∥ h T ∥ 1 ≤ 2 α ∥ h T c ∥ 1
(1-\sqrt{2}\alpha)\|h_T\|_1 \leq \sqrt{2}\alpha \|h_{T^c}\|_1
( 1 − 2 α ) ∥ h T ∥ 1 ≤ 2 α ∥ h T c ∥ 1
当
δ 2 k < 1 / 3 \delta_{2k}<1/3 δ 2 k < 1/3 1 − 2 α > 0 1-\sqrt{2}\alpha > 0 1 − 2 α > 0
∥ h T ∥ 1 ≤ 2 α 1 − 2 α ∥ h T c ∥ 1 ≜ C ~ ∥ h T c ∥ 1
\|h_T\|_1 \leq \frac{\sqrt{2}\alpha}{1-\sqrt{2}\alpha}\|h_{T^c}\|_1 \triangleq \tilde{C} \|h_{T^c}\|_1
∥ h T ∥ 1 ≤ 1 − 2 α 2 α ∥ h T c ∥ 1 ≜ C ~ ∥ h T c ∥ 1
再带入相应的项即证。不过,RIP
既然是更强的条件,它自然也有自己的长处。我们刚才证明了为了能够让压缩感知在有感知误差的时候也表现的
stable,RIP 是必要条件。实际上,RIP 同时也是充分条件。
定理 . 如果
A A A 2 k 2k 2 k δ 2 k < 2 − 1 \delta_{2k}<\sqrt{2}-1 δ 2 k < 2 − 1 x ^ \hat{x} x ^
min ∥ x ′ ∥ 1 , s . t . ∥ A x ′ − y ∥ ≤ ϵ
\min \|x'\|_1,\quad s.t. \|Ax'-y\|\leq \epsilon
min ∥ x ′ ∥ 1 , s . t .∥ A x ′ − y ∥ ≤ ϵ
其中
y = A x + e y = Ax + e y = A x + e ϵ ≥ ∥ e ∥ 2 \epsilon \geq \|e\|_2 ϵ ≥ ∥ e ∥ 2
∥ x ^ − x ∥ 2 ≤ C 0 σ k ( x ) 1 k + C 2 ϵ
\|\hat{x}-x\|_2 \leq C_0\frac{\sigma_k(x)_1}{\sqrt{k}} + C_2 \epsilon
∥ x ^ − x ∥ 2 ≤ C 0 k σ k ( x ) 1 + C 2 ϵ
其中
C 0 = 2 1 − ( 1 − 2 ) δ 2 k 1 − ( 1 + 2 ) δ 2 k , C 2 = 4 1 + δ 2 k 1 − ( 1 + 2 ) δ 2 k
C_0 = 2\frac{1-(1-\sqrt{2})\delta_{2k}}{1-(1+\sqrt{2})\delta_{2k}}, \quad C_2 = 4\frac{\sqrt{1+\delta_{2k}}}{1-(1+\sqrt{2})\delta_{2k}}
C 0 = 2 1 − ( 1 + 2 ) δ 2 k 1 − ( 1 − 2 ) δ 2 k , C 2 = 4 1 − ( 1 + 2 ) δ 2 k 1 + δ 2 k
证明可以参见 (Candes,
2008) 或者《Compressive
Sensing: Theory and Applications 》第一章中整理过的定理 1.9
的证明。关于这个定理,有几点需要注意的:
这个定理将之前的情况作为特殊情况包含进来。特别地,如果测量误差
ϵ \epsilon ϵ ℓ 2 \ell_2 ℓ 2 ℓ 1 \ell_1 ℓ 1 ℓ 2 \ell_2 ℓ 2
更进一步,如果
x x x k k k σ k ( x ) 1 = 0 \sigma_k(x)_1=0 σ k ( x ) 1 = 0 x ^ = x \hat{x}=x x ^ = x
这个定理和之前的结果不太一样的是,给出了一个切实可行的
decoder:也就是
ℓ 1 \ell_1 ℓ 1 ϵ = 0 \epsilon=0 ϵ = 0 ϵ ≠ 0 \epsilon\neq 0 ϵ = 0
小结一下,如果我们保证感知矩阵
A A A 2 k 2k 2 k ℓ 1 \ell_1 ℓ 1 ℓ 1 \ell_1 ℓ 1 n n n A A A 未完待续 吧!
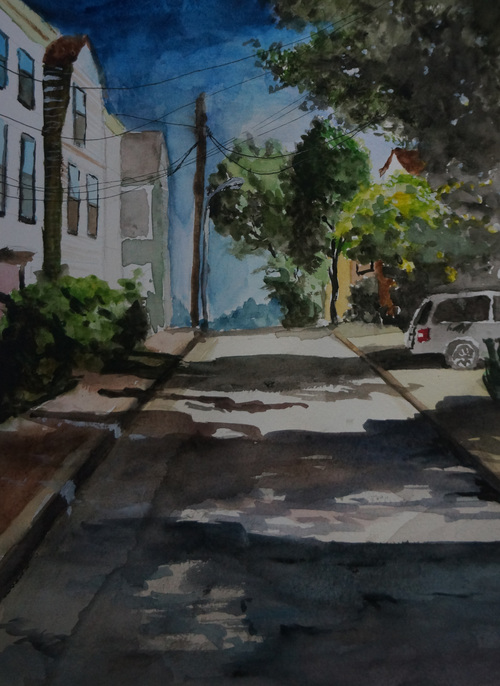
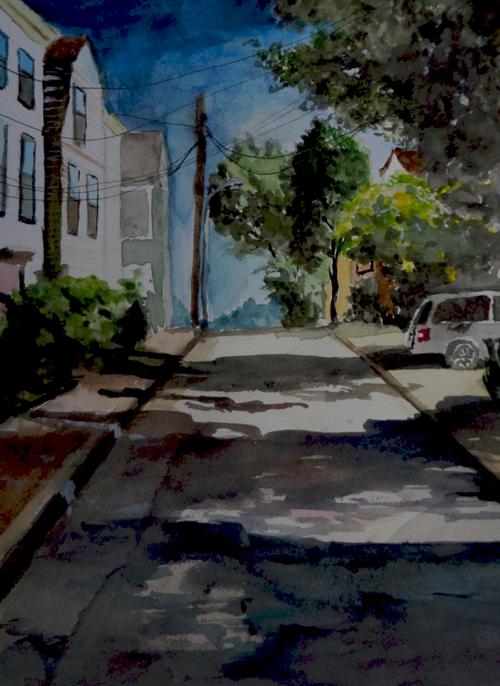

如果基于 Disqus 的评论系统无法加载,可以使用下面基于 Github 的评论系统(需要使用 Github 账号登陆)。