之前我们一直在讨论无约束的优化问题,定义域就是整个欧氏空间,不过在实际问题中我们经常需要解决带约束的优化问题。今天我们就来对带约束的优化问题做一个初步的介绍。在这里我们仍然假设所涉及的函数都是可导的,非光滑的优化问题将留到后面的篇幅来介绍。
带约束的优化问题的一般形式是
min x ∈ X f ( x )
\min_{x\in X} f(x)
x ∈ X min f ( x )
其中
X X X X X X X X X
min X r ∥ X − X r ∥ F 2 , s . t . rank ( X r ) ≤ r
\min_{X_r} \|X - X_r\|_F^2, \quad s.t. \text{rank}(X_r) \leq r
X r min ∥ X − X r ∥ F 2 , s . t . rank ( X r ) ≤ r
也就是要求一个矩阵
X X X ∥ X ∥ F = Tr ( X T X ) = ∑ i , j X i j 2 \|X\|_F = \sqrt{\text{Tr}(X^TX)} = \sqrt{\sum_{i,j}X_{ij}^2} ∥ X ∥ F = Tr ( X T X ) = ∑ i , j X ij 2 { X r : rank ( X r ) ≤ r } \{X_r:\text{rank}(X_r)\leq r\} { X r : rank ( X r ) ≤ r } X = U Σ V T X=U\Sigma V^T X = U Σ V T X X X Σ \Sigma Σ X X X U U U V V V Σ r \Sigma_r Σ r Σ \Sigma Σ r r r X r ∗ = U Σ r V T X_r^*=U\Sigma_r V^T X r ∗ = U Σ r V T r r r r + 1 r+1 r + 1
这里可以简单解释一下,注意到乘以一个正交矩阵只是进行基的旋转,并不改变矩阵的
Frobenius Norm,于是我们有
∥ X − X r ∥ F 2 = ∥ U Σ V T − X r ∥ F 2 = ∥ U T U Σ V T V − U T X r V ∥ F 2 = ∥ Σ − U T X r V ∥ F 2
\begin{aligned}
\|X - X_r\|_F^2 &= \|U\Sigma V^T - X_r\|_F^2 \\
&= \|U^TU\Sigma V^TV - U^TX_rV\|_F^2 \\
&= \|\Sigma - U^TX_rV\|_F^2
\end{aligned}
∥ X − X r ∥ F 2 = ∥ U Σ V T − X r ∥ F 2 = ∥ U T U Σ V T V − U T X r V ∥ F 2 = ∥Σ − U T X r V ∥ F 2
注意到
U T X r V U^TX_rV U T X r V r r r r r r r r r Matrix
Algorithms: Volume 1, Basic Decompositions 》的定理 4.32
(Schmidt-Mirsky)。
总而言之这里这个例子要说明的是,虽然我们会将精力主要集中在 convex set
constrained 优化问题上,但是并不代表 non-convex set constrained
优化问题在实际中不会出现或者不重要,更不代表这样的问题就是没有全局最优解或者是不能很有效地求解的。
接下来让我们再回到优化问题上,一般情况下,x ∈ X x\in X x ∈ X
min x f ( x ) s . t . g i ( x ) ≤ 0 , i = 1 , … , m h i ( x ) = 0 , i = 1 , … , l
\begin{aligned}
\min_x \;& f(x) \\
s.t. \;& g_i(x) \leq 0, \quad i = 1,\ldots,m \\
& h_i(x) = 0, \quad i=1,\ldots,l
\end{aligned}
x min s . t . f ( x ) g i ( x ) ≤ 0 , i = 1 , … , m h i ( x ) = 0 , i = 1 , … , l
当
f f f g i g_i g i h i h_i h i g i g_i g i { x : g i ( x ) ≤ 0 } \{x:g_i(x)\leq 0\} { x : g i ( x ) ≤ 0 } h i h_i h i { x : h i ( x ) = 0 } \{x:h_i(x)=0\} { x : h i ( x ) = 0 } h i h_i h i { x : h i ( x ) = 0 } \{x:h_i(x)=0\} { x : h i ( x ) = 0 }
作为一个具体的机器学习中的例子,让我们来考虑支持向量机 Support Vector
Machines (SVM)。我在之前写过一个比较详细的支持向量机系列 的介绍文章,不过这里让我们不妨来简单回顾一下。
问题的背景是有一系列数据点
x 1 , … , x N x_1,\ldots,x_N x 1 , … , x N y i ∈ { + 1 , − 1 } y_i\in\{+1,-1\} y i ∈ { + 1 , − 1 } w T x = b w^Tx = b w T x = b { x i } i = 1 N \{x_i\}_{i=1}^N { x i } i = 1 N y i = 1 y_i=1 y i = 1 x i x_i x i w T x − b = 0 w^Tx-b=0 w T x − b = 0
w T x i − b ∥ w ∥
\frac{w^Tx_i - b}{\|w\|}
∥ w ∥ w T x i − b
而
y i = − 1 y_i=-1 y i = − 1 w w w b b b ∥ w ∥ = 1 \|w\|=1 ∥ w ∥ = 1
max w , b , δ δ s . t . w T x i − b ≥ δ , y i = + 1 w T x i − b ≤ − δ , y i = − 1 ∥ w ∥ = 1
\begin{aligned}
\max_{w,b,\delta} \;&\delta \\
s.t. \;& w^Tx_i - b \geq \delta, \quad y_i = +1 \\
& w^Tx_i - b \leq -\delta, \quad y_i = -1 \\
& \|w\| = 1
\end{aligned}
w , b , δ max s . t . δ w T x i − b ≥ δ , y i = + 1 w T x i − b ≤ − δ , y i = − 1 ∥ w ∥ = 1
这已经是一个标准的带约束优化问题了。不过我们注意到
∥ w ∥ = 1 \|w\|=1 ∥ w ∥ = 1 ω = w / δ \omega = w/\delta ω = w / δ β = b / δ \beta = b/\delta β = b / δ
max ω , β , δ δ s . t . ω T x i − β ≥ 1 , y i = + 1 ω T x i − β ≤ − 1 , y i = − 1 ∥ ω ∥ = 1 δ
\begin{aligned}
\max_{\omega,\beta,\delta} \;&\delta \\
s.t. \;& \omega^Tx_i - \beta \geq 1, \quad y_i = +1 \\
& \omega^Tx_i - \beta \leq -1, \quad y_i = -1 \\
& \|\omega\| = \frac{1}{\delta}
\end{aligned}
ω , β , δ max s . t . δ ω T x i − β ≥ 1 , y i = + 1 ω T x i − β ≤ − 1 , y i = − 1 ∥ ω ∥ = δ 1
再做简单变化消掉变量
δ \delta δ
min ω , β ∥ ω ∥ s . t . ω T x i − β ≥ 1 , y i = + 1 ω T x i − β ≤ − 1 , y i = − 1
\begin{aligned}
\min_{\omega,\beta} \;&\|\omega\| \\
s.t. \;& \omega^Tx_i - \beta \geq 1, \quad y_i = +1 \\
& \omega^Tx_i - \beta \leq -1, \quad y_i = -1
\end{aligned}
ω , β min s . t . ∥ ω ∥ ω T x i − β ≥ 1 , y i = + 1 ω T x i − β ≤ − 1 , y i = − 1
到这里我们看到了熟悉的 SVM 的目标函数了(比较简单的没有带 slack
variable
的版本),并且此时所有约束都是线性的,我们可以很明显地看出这是一个凸优化问题。通常情况下为了求导方便目标函数会写成
∥ ω ∥ 2 \|\omega\|^2 ∥ ω ∥ 2 ∥ ω ∥ \|\omega\| ∥ ω ∥
现在让我们回到抽象的带约束优化问题上。回忆一下,在 unconstrained
优化问题中,我们证明了目标函数的 gradient
等于零是(局部)最优解的必要条件,并由此得出了 gradient descent
算法,通过不动点迭代来寻找 gradient 的零点。但是在 constrained
优化问题中,有可能出现的情况是目标函数 gradient
等于零的点是不能达到的,也就是说在约束集之外的,此时一般最优解会在约束集的边界上取到。总而言之
gradient
的零点不再是最优解的必要条件了,接下来我们将简要介绍一下在带约束的情况下如何来刻画最优解。
为了记号上方便,我们采用向量记法
g ( x ) = ( g 1 ( x ) , … , g m ( x ) ) g(x) = (g_1(x),\ldots,g_m(x)) g ( x ) = ( g 1 ( x ) , … , g m ( x )) h ( x ) = ( h 1 ( x ) , … , h l ( x ) ) h(x) = (h_1(x), \ldots,h_l(x)) h ( x ) = ( h 1 ( x ) , … , h l ( x ))
min x f ( x ) s . t . g ( x ) ⪯ 0 h ( x ) = 0
\begin{aligned}
\min_x \;& f(x) \\
s.t. \;& g(x) \preceq 0 \\
& h(x) = 0
\end{aligned}
x min s . t . f ( x ) g ( x ) ⪯ 0 h ( x ) = 0
注意这里的讨论中我们并没有要求这是一个 convex
优化问题,但是为了简单起见,我们假设
h ( x ) h(x) h ( x ) h ( x ) h(x) h ( x ) h ( x ) h(x) h ( x ) 隐函数定理 之类的工具来进行局部讨论,有点繁琐。于是我们索性将问题写作
min x f ( x ) s . t . g ( x ) ⪯ 0 A x − b = 0
\begin{aligned}
\min_x \;& f(x) \\
s.t. \;& g(x) \preceq 0 \\
& Ax - b = 0
\end{aligned}
x min s . t . f ( x ) g ( x ) ⪯ 0 A x − b = 0
接下来我们考虑一个比较直观的几何条件。假设我们在一个 feasible point
x ˉ \bar{x} x ˉ
1
定理 1 (Geometric
First-order Necessary Conditions) . 令
F 0 = { d ≠ 0 : ∇ f ( x ˉ ) T d < 0 } F_0 = \{d\neq 0: \nabla f(\bar{x})^T d < 0\} F 0 = { d = 0 : ∇ f ( x ˉ ) T d < 0 } I I I I = { i : g i ( x ˉ ) = 0 } I=\{i:g_i(\bar{x})=0\} I = { i : g i ( x ˉ ) = 0 } G 0 = { d ≠ 0 : ∇ g i ( x ˉ ) T d < 0 , ∀ i ∈ I } G_0=\{d\neq 0: \nabla g_i(\bar{x})^T d < 0, \forall i\in I\} G 0 = { d = 0 : ∇ g i ( x ˉ ) T d < 0 , ∀ i ∈ I } H 0 = { d ≠ 0 : A d = 0 } H_0=\{d\neq 0: Ad = 0\} H 0 = { d = 0 : A d = 0 } x ˉ \bar{x} x ˉ F 0 ∩ G 0 ∩ H 0 = ∅ F_0\cap G_0 \cap H_0 = \emptyset F 0 ∩ G 0 ∩ H 0 = ∅
该定理其实就是把我们刚才的 intuition
用数学语言陈述了一下。证明也非常简单,如果交集非空的话,我们任取交集中的一个方向
d d d x ˉ \bar{x} x ˉ
为此我们需要一些凸分析方面的工具,所以这里暂时“离题”介绍一些结论,因为可能以后也会用到这些结论,所以这里明确地给出来。
1
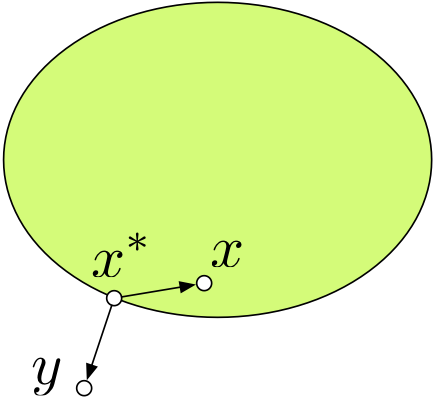
性质 1 . 设
S ⊂ R n S\subset\mathbb{R}^n S ⊂ R n y ∉ S y\not\in S y ∈ S
min x ∈ S ∥ x − y ∥
\min_{x\in S} \|x-y\|
x ∈ S min ∥ x − y ∥
存在唯一解
x ∗ x^* x ∗ x ∗ x^* x ∗
( y − x ∗ ) T ( x − x ∗ ) ≤ 0 , ∀ x ∈ S
(y-x^*)^T(x-x^*) \leq 0, \quad\forall x\in S
( y − x ∗ ) T ( x − x ∗ ) ≤ 0 , ∀ x ∈ S
从图
(fig:
2)
中来看这个结论所说的事情还是比较容易直观地记住的,证明并不复杂,我们就不在这里详细给出了。通过这个结论我们可以得出一系列的关于凸集的
separating hyperplane
的定理,根据凸集的开闭性、紧致性以及是凸集与点之间还是两个凸集之间会有各种不同的结论和变种。下面介绍一个我们马上会用到的版本。
2
定理 2 (Strong
Separation) . 设
S ⊂ R n S\subset \mathbb{R}^n S ⊂ R n y ∉ S y\not\in S y ∈ S w T x − b = 0 w^Tx-b=0 w T x − b = 0 ϵ > 0 \epsilon > 0 ϵ > 0 w T y − b ≥ ϵ w^Ty-b \geq \epsilon w T y − b ≥ ϵ x ∈ S x\in S x ∈ S w T x − b ≤ − ϵ w^Tx-b \leq -\epsilon w T x − b ≤ − ϵ S S S y y y
利用前面的命题中得到的结论,令
x ∗ x^* x ∗ y y y S S S ( y − x ∗ ) T x − ( y − x ∗ ) T x ∗ − ϵ = 0 (y-x^*)^Tx - (y-x^*)^Tx^* - \epsilon = 0 ( y − x ∗ ) T x − ( y − x ∗ ) T x ∗ − ϵ = 0 ϵ ≤ 0.5 ∥ y − x ∗ ∥ 2 \epsilon \leq 0.5\|y-x^*\|^2 ϵ ≤ 0.5∥ y − x ∗ ∥ 2
3
定理 3 (Farkas’
Lemma) . 设
A ∈ R m × n A\in\mathbb{R}^{m\times n} A ∈ R m × n c ∈ R n c\in \mathbb{R}^n c ∈ R n
A x ⪯ 0 Ax\preceq 0 A x ⪯ 0 c T x > 0 c^Tx > 0 c T x > 0 A T y = c A^Ty = c A T y = c y ≥ 0 y\geq 0 y ≥ 0
这个定理初看有些莫名其妙,简单解释一下。考虑
A A A A 1 , … , A m A_1,\ldots,A_m A 1 , … , A m x x x A 1 , … , A m A_1,\ldots,A_m A 1 , … , A m c c c A A A c c c
第二条有解说的是存在一个非负权重,使得
c c c A 1 , … , A m A_1,\ldots,A_m A 1 , … , A m c ∈ cone ( A 1 , … , A m ) c\in \text{cone}(A_1,\ldots,A_m) c ∈ cone ( A 1 , … , A m )
这样从几何的角度来解释之后 Farkas’ Lemma
其实还是挺直观的,实际上我们正是要用 Farkas’ Lemma
将代数和几何联系起来。我们这里省略证明,主要的麻烦的地方在于要证明一个构造出来的凸集是闭的,之后直接运用上面的
strong separation 结论就可以证明了。具体可以参见《Nonlinear
Programming 》的内容。
4
定理 4 (Fritz John
Necessary Conditions) . 设
x ˉ \bar{x} x ˉ u 0 u_0 u 0 u u u v v v
u 0 ∇ f ( x ˉ ) + ∇ g ( x ˉ ) T u + A T v = 0 u 0 , u ≥ 0 , ( u 0 , u , v ) ≠ 0 u i g i ( x ˉ ) = 0 , i = 1 , … , m
\begin{aligned}
&u_0\nabla f(\bar{x}) + \nabla g(\bar{x})^T u + A^Tv = 0 \\
&\quad u_0,u\geq 0, (u_0,u,v)\neq 0 \\
&\quad u_ig_i(\bar{x}) = 0, i=1,\ldots, m
\end{aligned}
u 0 ∇ f ( x ˉ ) + ∇ g ( x ˉ ) T u + A T v = 0 u 0 , u ≥ 0 , ( u 0 , u , v ) = 0 u i g i ( x ˉ ) = 0 , i = 1 , … , m
根据
(thm:
1) ,F 0 ∩ G 0 ∩ H 0 = ∅ F_0\cap G_0 \cap H_0=\emptyset F 0 ∩ G 0 ∩ H 0 = ∅ d d d
∇ f ( x ˉ ) T d < 0 ∇ g i ( x ˉ ) T d < 0 , i ∈ I A d = 0
\begin{aligned}
&\nabla f(\bar{x})^T d < 0 \\
&\nabla g_i(\bar{x})^T d < 0, \quad i\in I\\
&Ad = 0
\end{aligned}
∇ f ( x ˉ ) T d < 0 ∇ g i ( x ˉ ) T d < 0 , i ∈ I A d = 0
令
∇ g I ( x ˉ ) = ( ∇ g i ( x ˉ ) ) i ∈ I \nabla g_I(\bar{x})=(\nabla g_i(\bar{x}))_{i\in I} ∇ g I ( x ˉ ) = ( ∇ g i ( x ˉ ) ) i ∈ I
B = [ ∇ f ( x ˉ ) T ∇ g I ( x ˉ ) T ]
B = \begin{bmatrix}\nabla f(\bar{x})^T \\ \nabla g_I(\bar{x})^T\end{bmatrix}
B = [ ∇ f ( x ˉ ) T ∇ g I ( x ˉ ) T ]
则如下 system 无解
B x + e θ ⪯ 0 , θ > 0 A x ⪯ 0 − A x ⪯ 0
\begin{aligned}
Bx + e\theta &\preceq 0, \quad \theta > 0 \\
Ax &\preceq 0\\
-Ax &\preceq 0
\end{aligned}
B x + e θ A x − A x ⪯ 0 , θ > 0 ⪯ 0 ⪯ 0
变换一下形式
[ B e A 0 − A 0 ] [ x θ ] ⪯ 0 , [ 0 1 ] T [ x θ ] > 0
\begin{bmatrix} B & e \\ A & 0 \\ -A & 0\end{bmatrix}\begin{bmatrix}x \\ \theta \end{bmatrix} \preceq 0,\quad \begin{bmatrix} 0 \\ 1 \end{bmatrix}^T \begin{bmatrix}x \\ \theta \end{bmatrix} > 0
B A − A e 0 0 [ x θ ] ⪯ 0 , [ 0 1 ] T [ x θ ] > 0
于是根据刚才的 Farkas’ Lemma,我们知道存在
y = ( u 0 , u I , v + , v − ) ⪰ 0 y=(u_0,u_I,v^+, v^-)\succeq 0 y = ( u 0 , u I , v + , v − ) ⪰ 0
u 0 ∇ f ( x ˉ ) + ∇ g I ( x ˉ ) T u I + A ( v + − v − ) = 0 u 0 + e T u = 1
\begin{aligned}
u_0\nabla f(\bar{x}) + \nabla g_I(\bar{x})^Tu_I + A(v^+-v^-) &= 0 \\
u_0 + e^Tu &= 1
\end{aligned}
u 0 ∇ f ( x ˉ ) + ∇ g I ( x ˉ ) T u I + A ( v + − v − ) u 0 + e T u = 0 = 1
令
v = v + − v − v=v^+-v^- v = v + − v − u u u I I I
不过 Frtiz John 条件在
∇ f ( x ˉ ) \nabla f(\bar{x}) ∇ f ( x ˉ ) u 0 u_0 u 0 u 0 > 0 u_0>0 u 0 > 0 u 0 u_0 u 0
− ∇ f ( x ˉ ) = ∇ g ( x ˉ ) T u / u 0 + A T v / u 0
-\nabla f(\bar{x}) = \nabla g(\bar{x})^T u/u_0 + A^T v/u_0
− ∇ f ( x ˉ ) = ∇ g ( x ˉ ) T u / u 0 + A T v / u 0
此时可以理解成目标函数的 gradient 向量的相反方向由 constraints 的
gradient 线性张成,并且考虑不等式 constraints 的话,由于
u ≥ 0 u\geq 0 u ≥ 0
为了做到这一点,注意到 Fritz John 条件里已经有了
u 0 ≥ 0 u_0\geq 0 u 0 ≥ 0 u 0 = 0 u_0=0 u 0 = 0 u 0 = 0 u_0=0 u 0 = 0
∇ g ( x ˉ ) T u + A T v = 0 , ( u , v ) ≠ 0
\nabla g(\bar{x})^T u + A^Tv = 0, \quad (u,v) \neq 0
∇ g ( x ˉ ) T u + A T v = 0 , ( u , v ) = 0
也就是说等式和不等式的 constraints 的 gradient
是线性相关的。因此如果我们能保证它们线性无关的话,就可以排除这种情况。于是有如下结论。
5
定理 5 (Karush-Kuhn-Tucker (KKT) Necessary Conditions) . 设
x ˉ \bar{x} x ˉ ∇ g i ( x ˉ ) , i ∈ I \nabla g_i(\bar{x}), i\in I ∇ g i ( x ˉ ) , i ∈ I A A A u , v u,v u , v
∇ f ( x ˉ ) + ∇ g ( x ˉ ) T u + A T v = 0 u ⪰ 0 u i g i ( x ˉ ) = 0 , i = 1 , … , m
\begin{aligned}
\nabla f(\bar{x}) + \nabla g(\bar{x})^T u + A^Tv &= 0 \\
u &\succeq 0 \\
u_i g_i(\bar{x}) &= 0, \quad i = 1, \ldots, m
\end{aligned}
∇ f ( x ˉ ) + ∇ g ( x ˉ ) T u + A T v u u i g i ( x ˉ ) = 0 ⪰ 0 = 0 , i = 1 , … , m
这就是我们常见的 KKT 条件,成立的条件是
x ˉ \bar{x} x ˉ
6
定理 6 (Slater
Condition) . 如果
g i ( x ) g_i(x) g i ( x ) A A A x x x g i ( x ) < 0 g_i(x)<0 g i ( x ) < 0
7
定理 7 (Linear
Constraints) . 如果所有 constraints 都是线性的,那么 KKT
条件是局部最优解的必要条件。
注意以上两个结论中都并没有要求目标函数
f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x ) g i ( x ) g_i(x) g i ( x )
8
定理 8 (KKT Sufficient
Conditions for Convex Problems) . 设
x ˉ \bar{x} x ˉ u , v u,v u , v ∇ f ( x ˉ ) + ∇ g ( x ˉ ) T u + A T v = 0 u ⪰ 0 u i g i ( x ˉ ) = 0 , i = 1 , … , m
\begin{aligned}
\nabla f(\bar{x}) + \nabla g(\bar{x})^T u + A^Tv &= 0 \\
u &\succeq 0 \\
u_i g_i(\bar{x}) &= 0, \quad i = 1, \ldots, m
\end{aligned}
∇ f ( x ˉ ) + ∇ g ( x ˉ ) T u + A T v u u i g i ( x ˉ ) = 0 ⪰ 0 = 0 , i = 1 , … , m f ( x ) f(x) f ( x ) g i ( x ) , i = 1 , … , m g_i(x), i=1,\ldots,m g i ( x ) , i = 1 , … , m x ˉ \bar{x} x ˉ
到这里为止几乎未加证明地介绍了许多结论了,让我们简单地带入 SVM
的问题中小结一下结束本篇文章。这里我们再对 SVM
问题做一些简单的变换,一个是用
1 / 2 ∥ ω ∥ 2 1/2\|\omega\|^2 1/2∥ ω ∥ 2 ∥ ω ∥ \|\omega\| ∥ ω ∥
min ω , β 1 2 ∥ ω ∥ 2 s . t . y i ( ω T x i − β ) ≥ 1 , i = 1 , … , N
\begin{aligned}
\min_{\omega, \beta} \;&\frac{1}{2}\|\omega\|^2 \\
s.t. \;& y_i(\omega^Tx_i - \beta) \geq 1, \quad i = 1,\ldots, N
\end{aligned}
ω , β min s . t . 2 1 ∥ ω ∥ 2 y i ( ω T x i − β ) ≥ 1 , i = 1 , … , N
首先该问题显然是 convex 的,因此 KKT 条件是充分条件。然后 Slater
point
的存在性其实就是看数据是否严格线性可分,也就是说是否存在一个超平面
ω T x − β = 0 \omega^Tx-\beta =0 ω T x − β = 0 y i ( ω T x i − β ) > 1 y_i(\omega^Tx_i-\beta) > 1 y i ( ω T x i − β ) > 1
ω − ∑ i = 1 N u i y i x i = 0 u i ≥ 0 , i = 1 , … , N u i ( 1 − y i ( ω T x i − β ) ) = 0 , i = 1 , … , N
\begin{aligned}
\omega - \sum_{i=1}^N u_i y_ix_i &= 0 \\
u_i &\geq 0, \quad i=1,\ldots, N \\
u_i \left( 1 - y_i(\omega^Tx_i-\beta) \right) &= 0, \quad i = 1,\ldots, N
\end{aligned}
ω − i = 1 ∑ N u i y i x i u i u i ( 1 − y i ( ω T x i − β ) ) = 0 ≥ 0 , i = 1 , … , N = 0 , i = 1 , … , N
如果将
u i u_i u i SVM 的 dual 推导 里的
dual 变量联系起来的话,其中第一条实际上是给出了关于结果的 separating
hyperplane 的法向量
ω \omega ω x ~ \tilde{x} x ~
ω T x ~ − β = ∑ i = 1 N u i y i ⟨ x i , x ~ ⟩ − β
\omega^T\tilde{x} - \beta = \sum_{i=1}^N u_iy_i\langle x_i, \tilde{x}\rangle - \beta
ω T x ~ − β = i = 1 ∑ N u i y i ⟨ x i , x ~ ⟩ − β
只涉及到
x i x_i x i x ~ \tilde{x} x ~ u i ≥ 0 u_i\geq 0 u i ≥ 0 x i x_i x i x i x_i x i y i ( ω T x i − β ) > 1 y_i(\omega^Tx_i-\beta) > 1 y i ( ω T x i − β ) > 1 u i u_i u i u i = 0 u_i=0 u i = 0
最后小结一下,优化问题的最优解的充分条件和必要条件各自有什么用处。我们目前还没有涉及到任何实际的求解算法,但是必要条件一般可以用来寻找可能的最优解,因为最优解如果存在的话,一定会满足必要条件,因此一个比较暴力的办法就是直接枚举所有符合必要条件的解寻找最优的那一个。有些问题可以比较直接地解出满足必要条件的点,而令一些问题可能需要更多地步骤,例如在之前介绍的
unconstrained
优化问题中就是通过不动点迭代去寻找对应的必要条件(目标函数的 gradient
等于零)的点。而反过来,充分条件则有时候不是想象中的那么有用:如果你刚巧拿到了一个解并且这个解刚巧满足了充分条件的话,那么就皆大欢喜了:恭喜你找到了最优解。但是如果不满足充分条件的话,就说不清楚了,它既有可能是最优解也有可能不是。

如果基于 Disqus 的评论系统无法加载,可以使用下面基于 Github 的评论系统(需要使用 Github 账号登陆)。