上一次我们介绍了带约束的优化问题，以及局部最优解的充分条件和必要条件，这一次我们要介绍一个具体的算法，当 constraints 对应一个 convex set，并且计算到该集合的投影非常容易的时候，我们可以用一种叫做 Projected Gradient Method 的迭代算法来进行优化求解。具体来说，今天我们考虑这样的问题：

$$\min_{x\in S}\; f(x)$$

其中 $S$ 是非空闭凸集。上一次分析带约束优化问题的充分必要条件的时候我们将约束写成具体的等式和不等式的形式，这次我们只表示成抽象的 $x\in S$ 的形式，因为我们并不关心其约束集的具体描述形式，只要假设有一个 blackbox 的投影算子 $P_S(x)$，能计算 $\arg\min_{y\in S}\|x-y\|$ 即可。

Projected Gradient Method 其实非常简单，只是在普通的 Gradient Descent 算法中间多加了一步 projection 的步骤，保证解在 feasible region 里面。这个方法看起来似乎只是一个很 naive 的补丁，不过实际上是一个很正经的算法，可以用类似的方法证明其收敛性和收敛速度都和普通的 Gradient Descent 差不多。

首先我们要说明投影算法的可行性。具体来说，要计算投影，我们必须要有投影的存在性和唯一性。这个实际上在上一次的性质 1 中给出来了。方便起见我们在这里再重复一次，为了本文方便也把记号稍微变一下。

由于这个结论对本文来说比较重要，我们在这里简单证明一下。首先存在性和唯一性是由 $S$ 是非空闭凸集以及 norm 是严格凸函数得到的可以任取 $S$ 内的一点 $x'$，以 $x$ 为中心 $\|x-x'\|$ 为半径作一个球，与 $S$ 相交得到一个紧的非空凸集，从而保证最优解的存在性。。考虑当 $x\in S$ 的时候，显然最优解就是 $x_S=x$ 本身。此时性质中所对应的式子是 trivially 满足的。反过来如果该式子成立，由于 $x\in S$，带入式子中，可以得到

$$\|x-x_S\|^2 \leq 0$$

因此 $x=x_S$。所以当 $x\in S$ 的时候充要条件成立。接下来考虑 $x\not\in S$ 的情况。首先证明必要性。用反证法，假设 $x_S$ 是投影点，但是不等式不满足，亦即存在 $y\in S$ 使得

$$(x-x_S)^T(y-x_S) > 0$$

此时考虑 $x_\theta = x_S + \theta (y - x_S)$，其中 $\theta \in [0,1]$，根据 $S$ 的 convexity，有 $x_\theta \in S$。接下来我们要证明 $x_\theta$ 可以比 $x_S$ 更优，以导出矛盾。

$$\begin{aligned} \|x-x_\theta\|^2 &= \|x - x_S - \theta (y-x_S)\|^2 \\ &= \|x-x_S\|^2 - 2\theta (x-x_S)^T(y-x_S) + \theta^2 \|y-x_S\|^2 \end{aligned}$$

由于 $\theta^2$ 比 $\theta$ 更加快速地趋向于 0，且 $\theta$ 那一项的系数是严格负的，所以当 $\theta$ 足够小时，我们可以得到

$$- 2\theta (x-x_S)^T(y-x_S) + \theta^2 \|y-x_S\|^2 < 0$$

也就是说 $\|x-x_\theta\|^2 < \|x-x_S\|^2$，矛盾。接下来考虑充分性，假设该不等式对任意 $y\in S$ 成立，为了证明 $x_S$ 是最优解，考虑任意的 $y \in S$，我们有

$$\begin{aligned} \|x-y\|^2 &= \|x-x_S + x_S - y\|^2 \\ &= \|x-x_S\|^2 - 2(x-x_S)^T(y-x_S) + \|x_S-y\|^2 \\ &\geq \|x-x_S\|^2 + \|x_S-y\|^2 \end{aligned}$$

其中最后一步是根据条件中的不等式得到的。当 $y\neq x_S$ 时，$\|x_S-y\|^2>0$，此时我们可以得到

$$\|x-y\|^2 > \|x-x_S\|^2$$

根据 $y$ 的任意性，即证明 $x_S$ 是最优解。

当然，有了投影的存在性和唯一性并不代表该投影是很容易计算的。对于一些有特定结构的集合 $S$，可能会有专门的算法可以计算投影或者甚至有最优解。例如上一次作为例子介绍的 SVM 的目标函数中的 constraints 就是由每一个数据点对应的一个线性不等式所描述的 half space 相交得到的一个 polyhedron，计算该投影虽然有专门的算法，但是也称不上特别容易。所以本文我们暂时不用 SVM 的例子，而是考虑更简单的情况。其中最简单的例子就是所谓的 non-negative cone：$S=\{x: x\succeq 0\}$，此时投影只要分别将每一维投影到非负半轴上就可以了，也就是令 $x_i\leftarrow \max\{x_i,0\}$。

不过，介绍具体的例子之前，让我们先回到 Projected Gradient Method 本身。假设我们现在有一个 blackbox 可以很容易地计算 $P_S(x)$，则算法由根据下迭代规则进行迭代直到收敛为止：

• $\bar{x}_k = P_S\left( x_k - s_k \nabla f(x_k) \right)$, $s_k>0$
• $x_{k+1} = x_k + \alpha_k (\bar{x}_k - x_k)$, $\alpha_k\in (0,1]$

其中 $s_k> 0$ 是一个步长参数，例如取 $\alpha_k = 1$ 的时候，上面的算法其实就变成了如下的迭代：

• $x_{k+1} = P_S\left( x_k - s_k \nabla f(x_k) \right)$

也就是通过一次普通的 gradient descent 然后再利用 Projection Operator $P_S(\cdot)$ 投影到 feasible set 里来。加上 $\alpha_k$ 参数之后实际上就是再多加了一步步长选择或者 line search 的过程，我们要求 $\alpha_k \in (0, 1]$ 这样可以保证不会再移动到 feasible set 外面去。

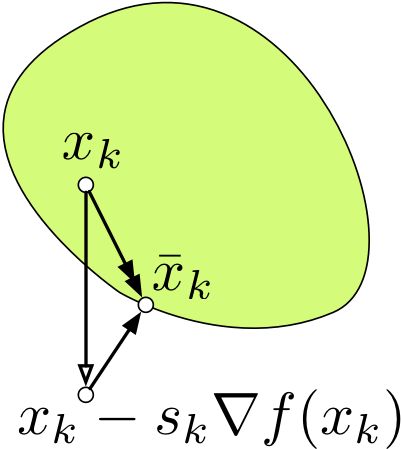
另外有一点值得一提的是，投影之后的移动方向 $\bar{x}_k - x_k$ 一定是一个下降方向：也就是说它和 $-\nabla f(x_k)$ 成锐角。这是因为根据刚才证明的性质中投影算子的最优解的充要条件的不等式得到的，另外从图中可以比较直观地看出来。

除此之外，在类似的前提条件下，我们也可以和像 unconstrained optimization 中证明梯度下降算法的收敛性一样证明 Projected Gradient Method 的收敛性。回忆一下我们在第一篇证明简单的固定步长的梯度下降的收敛性的时候，是证明了每次迭代中

$$\|x_{k+1}-x^*\| \leq M \|x_k - x^*\|$$

其中 $x^*$ 是最优解，而 $M$ 是一个严格小于 1 的正数。此时我们得到迭代法 Q-线性收敛到最优解。现在我们多了一步投影的步骤，在同样的前提假设下（此时上面的式子是成立的），我们有

图 1投影算子是 contraction 的几何证明。

$$\begin{aligned} \|P_S(x_{k+1}) - x^*\| &= \|P_S(x_{k+1}) - P_S(x^*)\| \\ &\leq \|x_{k+1}-x^*\| \\ &\leq M \|x_k - x^*\| \end{aligned}$$

其中第一个等式是因为 $x^*\in S$，随后的不等式是因为投影算子是一个 Contraction，也就是说：

这个性质有一个比较直观的几何证明，简单描述的话如图 (fig: 1) 所示，考虑 $x$ 和 $y$ 以及它们到 $S$ 的投影 $x_S$、$y_S$，以 $x_S-y_S$ 向量为法向量作两个分别通过 $x_S$ 和 $y_S$ 的超平面 $H_x$ 和 $H_y$。我们知道 $\|x_S-y_S\|$ 是两个超平面之间的距离，也就是超平面上的两个点之间的最短距离，而 $x$ 和 $y$ 两个点根据性质 (prop: 1) 分别在两个超平面上或者“外面”，因此它们两点的距离不会小于两个超平面之间的距离，也就是 $\|x_S-y_S\|$，即证。

现在回到我们的 Projected Gradient Method 上来。刚才的不等式中我们得到的结论是，由于投影算子是 Contraction，所以虽然多加了这一个步骤，但是并不会影响我们以前关于 gradient method 的收敛性的证明，所有步骤几乎可以原封不动地用到这个方法中来。

介绍完优化算法之后，同以往一样，我们将它用到一个机器学习的模型中去。从刚才的介绍和分析上可以看到，这个算法不论从计算步骤还是分析本身都只比普通的 gradient descent 多了一步而已，得到的收敛复杂度也是一样的，不过需要再次强调的是，这里的收敛复杂度是一迭代次数来计算的，我们一直都假设投影算子的计算是简单的，如果投影算子的计算本身就需要解一个复杂的优化问题的话，那么这样比较的意义就不大了。这里我们举一个投影算子非常容易计算的例子：LASSO。

LASSO 是在 sparsity 相关的问题中应用非常广泛的一个模型，具体来说，LASSO 对应如下的一个优化问题：

$$\min_w \; \sum_{i=1}^N (w^Tx_i - y_i)^2 + {\color{red}{\lambda\sum_{j=1}^n |w^j|}}$$

这里 $x_i$ 是数据，$y_i$ 是对应的值，该优化问题是用线性回归去拟合给定的数据，而向量 $w\in\mathbb{R}^n$，也就是我们的优化变量是拟合的线性模型参数，而红色的项是 regularizer，其中 $w^j$ 表示向量 $w$ 的第 $j$ 个 component，所有 component 的绝对值之和即 $w$ 的 $\ell_1$-norm，通过添加 $\ell_1$ regularizer 可以带来稀疏性，当 regularizer 系数 $\lambda$ 控制得当的时候最优解 $w$ 的很多 component 将会是零。

LASSO 问题的解法有很多，例如用 LARS 可以一次性解出所有可能的 $\lambda$ 取值所对应的解 $w$，这对于需要对 $\lambda$ 进行 cross-validation 调参数的情况来说非常省时省力，不过今天我们我们的目的是为了给 Projected Gradient Method 进行示例，所以不会在这里介绍 LARS 对应的算法。

话虽如此，但 LASSO 问题其实是一个 unconstrained 优化问题，但是由于其 regularizer 中的 $\ell_1$-norm 不可导，所以我们既不能套用之前讲过的简单的 Gradient Descent 算法不可导的优化问题的解法相关的内容将会在以后陆续介绍。，也不能直接套用这里讲到的 Projected Gradient Method，所以需要对问题做一下小小的变形。

这里其实就涉及到了 optimization 中很重要的一个环节：problem reformulation。一般解决一个问题可以分为以下几个步骤

1. 抽象问题，提出模型，建立目标函数
2. 将目标函数转化为易于求解的形式
3. 找到或者设计对应的优化算法
4. 编程、调试、跑实验，看着 cpu 实时利用率图发呆等

其中第一步是属于特定的问题领域相关的知识和技术，而最后一部则属于 computer engineering 相关的内容。第三步显然是 optimization 的覆盖范围，但是几乎同等重要的第二步实际上也是属于优化范畴的，并且通常被轻视的一环。大概也因为这其实也是比较困难的、没有什么比较系统的方法或者规律可循的一环的缘故吧。

回到 LASSO 问题，注意到任意实数 $w^j$ 都可以表示成其正部和负部之差 $w^j=w^j_+ - w^j_-$，其中 $w^j_+ = \max\{w^j,0\}\geq 0$, $w^j_-=\max\{-w^j,0\}\geq 0$。此时绝对值可以简单地表示成 $|w^j|=w^j_+ + w^j_-$。根据这个性质，我们在 LASSO 问题中引入新的变量 $w^j_+, w^j_0\geq 0$，$j=1,\ldots,n$，很容易可以证明，LASSO 问题等价于

$$\begin{aligned} \min_{w_+,w_-} \quad& \sum_{i=1}^N \left( (w_+-w_-)^Tx_i - y_i \right)^2 + \lambda \sum_{j=1}^n (w^j_++w^j_-) \\ s.t. \quad& w_+\succeq 0, w_-\succeq 0 \end{aligned}$$

现在问题变成了 constrained 优化问题，并且目标函数是可导的（二次函数），约束集也是投影算子非常容易计算的 non-negative cone。简直就是为我们今天准备的模范例子！

为了码代码方便我们把上面的目标函数写成矩阵形式：

$$\begin{aligned} \min_{w_+,w_-} \quad& \|Xw_+ - Xw_- - y\|^2 + \lambda w_+^T\mathbf{1} + \lambda w_-^T\mathbf{1} \\ s.t. \quad& w_+\succeq 0, w_-\succeq 0 \end{aligned}$$

其中 $X=(x_1,\ldots,x_N)^T$ 是数据矩阵。我们进一步令 $\tilde{w}=(w_+^T,w_-^T)^T$，$\tilde{X} = (X, -X)$，则问题的形式可以进一步简化为

$$\begin{aligned} \min_{\tilde{w}} \quad& \|\tilde{X}\tilde{w} - y\|^2 + \lambda \tilde{w}^T\mathbf{1} \\ s.t. \quad& \tilde{w}\succeq 0 \end{aligned}$$

这样一来 gradient 的计算和投影的计算都变得非常明了了。接下来我们把学到的只是用的一个具体的例子里。今天我们选一个信号处理里的例子：利用 natural image 在 wavelets 下的稀疏性来去除白噪声。

为了和刚才的记号尽量保持一致，我们用 $y$ 来表示一张图像，简单起见我们考虑灰度图像，也就是一个单通道的矩阵，不妨将 $y$ 看成是把该矩阵的每一列接起来得到的一个长向量。而正交的 discrete wavelet transform (DWT) 通过一组正交基 $W$ 可以将图像表示成系数 $w$ 的形式： $y = Xw$。

图 2加成白噪声的 lena 图像。

同时我们知道 natural image 和 wavelets 的性质：natural image 经过 DWT 之后得到的系数具有稀疏性——也就是说 $w$ 是一个稀疏向量。这个稀疏性有很多通途，比如用于存储和传输，由于很多 component 是零，不需要进行存储，因此可以节省很多存储空间。在 JPEG 2000 标准中就用到了 DWT。更细节的东西可以参考 DWT 的 wikipedia 页或者相关的书籍资料。

另一方面，图像白噪声，也就是随机的 Gaussian noise （图 (fig: 2) 是一个加成了白噪声的 lena 照片的示例）在 wavelet 变换下却并没有什么规律，或者说，其实还是白噪声，因为正交线性变换下高斯分布还是会得到高斯分布。图 (fig: 3) 是对比原始的 lena 图在 DWT 下的系数和白噪声加成之后的 DWT 系数的结果。可以看到白噪声严重破坏了稀疏性。

图 3(左) Lena 和 (右) Lena 加白噪声在 DWT 下的系数。

所幸的是白噪声所对应的系数绝对值都比较小，因此有一种非常简单的去白噪声的算法就是：将被白噪声污染的照片进行 DWT 得到变换后的系数，然后直接设定一个比较小的数作为阈值，将所有绝对值小于这个数的系数直接设为零，然后再进行逆向 DWT 得到去噪后的图片。

不过我们今天使用的是看起来略微“高端”一点的算法：我们通过 $\ell_1$-norm regularization 而不是直接 hard thresholding 来获得稀疏性。具体来说，令 $X$ 是 DWT 所对应的 wavelet 基，$y$ 是加上了白噪声的图片，我们通过求解下面的优化问题

$$\min_w \|Xw - y\|^2 + \lambda \|w\|_1$$

来得到一个稀疏的系数 $w$，最后再通过逆向小波变换将 $w$ 变回图像域，得到去噪后的图片。图 (fig: 4) 是 lena 原图和通过我们刚才描述的算法，用 Projected Gradient Method 求解后得到的结果对比。

原图。

带噪音的图。

去噪结果。

图 4Lena 去噪结果对比图。

可以看到去噪效果还算过得去吧，不少噪音抹平了，但是图片本身的内容也有不小的损失。当然这是相当 naive 的去噪方法，只用到了 natural image 在小波基下的系数的稀疏性这样的基本性质。

最后值得一提的是，虽然这个示例的优化问题中的目标函数是写成矩阵相乘的形式，但是在具体的实现中计算 gradient 以及目标函数值的时候并不需要先展开整个 wavelet 基矩阵然后用矩阵向量相乘，而只需要有一个 blackbox 算法可以执行快速的 wavelet transform 以及其逆向 transform 就可以了，通常速度会快很多。本文示例的 julia 代码类似地可以在我的 MLOpt.jl 代码 repo 对应本文的 release 下可以找到。详细参见 example/pgd_lena.jl 文件。